Table of Contents

• Prequiz...
• The Power Function
• 1: Introduction
• 2: What are scaling relationships?
• 3: The power function
• 4: The shape of the power function
• 5: The conversion factor "a"
• 6: The power factor "b"
• Log Transformations
• 7: Introduction
• 8: What are logarithms again?
• 9: Graphing on a log scale
• 10: Visualizing the data
• 11: Getting to a straight line
• 12: The key parameter is "b"
• The value of "b"
• 13: Introduction
• 14: A geometric approach
• 15: Scaling surface area of cubes
• 16: Scaling surface area of cubes
• 17: A "2/3 scaling law"?
• Confronting ideas with data
• 18: Introduction
• 19: An unexpected result
• 20: A "3/4 scaling law"?
• 21: Internal transport systems
• 22: Branching and supply networks
• 23: Deriving the "3/4 scaling law"
• 24: So what's the real value of "b"?
• Review
• 25: Review of Concepts

So, what is the real value of "b"?

Brown et al. claim that they have come up with a convincing reason why "b" has been found to be equal to 3/4. A value that they claim has been demonstrated over many studies and throughout several decades. Their theory is certainly convoluted and hard to understand (and we spared you almost all of the really gory details!). But they do claim to be able to derive a whole host of scaling laws, all of which scale to multiples of 1/4 (like the heart beat and life span example given earlier), and that gives a lot of support to their argument. And there is no other convincing theory that explains the pattern!

Recently, however, several authors have shown that there is still a great deal of uncertainty about the real value of "b". Is it really 3/4 as so many studies seem to suggest? Or is it possible that it is actually 2/3, as everyone originally thought it would be? How easy is it to tell 3/4 from 2/3 anyway? I mean, if you think about it, they are not so far from each other: 2/3 is equal to 0.67 and 3/4 is equal to 0.75 - a mere separation of 0.08. Can we really distinguish those two slopes?

Let's take a look at all our mammal data, using a fit scaled to both a 3/4 and 2/3 rule - what do we see?

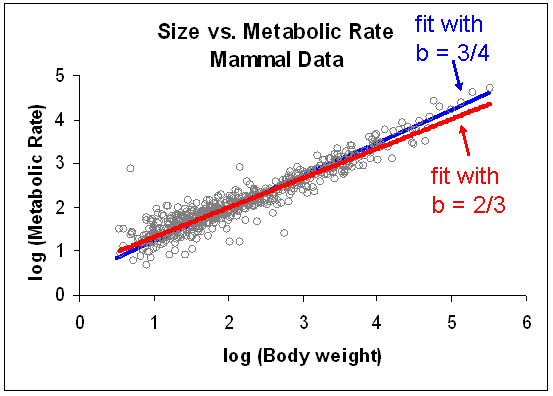
As you can see, these two lines are very close to each other. And statistical analysis of these kinds of data is very tricky - there is a lot of uncertainty in the parameter estimates - and recent publications in leading journals suggest that we can't really say whether the real scaling exponent is 2/3 or 3/4. But there are certainly many scientists convinced of the 3/4 scaling rule. Are they right or wrong? How can you tell?

Although we all like easy answers sometimes, these kinds of controversies are what drives science forward. And the introduction of Brown et al.'s theory has restimulated this area of study. As time goes on, their reasoning will be reexamined, more data will be brought to bear - and the scientific community will likely come to some sort of a consensus (we hope!). We'll just have to wait and see.