Table of Contents

• Prequiz...
• The Power Function
• 1: Introduction
• 2: What are scaling relationships?
• 3: The power function
• 4: The shape of the power function
• 5: The conversion factor "a"
• 6: The power factor "b"
• Log Transformations
• 7: Introduction
• 8: What are logarithms again?
• 9: Graphing on a log scale
• 10: Visualizing the data
• 11: Getting to a straight line
• 12: The key parameter is "b"
• The value of "b"
• 13: Introduction
• 14: A geometric approach
• 15: Scaling surface area of cubes
• 16: Scaling surface area of cubes
• 17: A "2/3 scaling law"?
• Confronting ideas with data
• 18: Introduction
• 19: An unexpected result
• 20: A "3/4 scaling law"?
• 21: Internal transport systems
• 22: Branching and supply networks
• 23: Deriving the "3/4 scaling law"
• 24: So what's the real value of "b"?
• Review
• 25: Review of Concepts

The conversion factor "a"

What does the "a" do in our equation

Metabolic rate = a * (size)^b

First, lets think about a simpler version of our equation (when b=1):

Metabolic rate = a* size¹ = a*size

Well, first off you may notice that you have an equation that says that metabolic rate equals size. That is an odd concept right there! Well, it turns out that one of the functions of "a" is to convert size into values that are appropriate for metabolic rate. That's why we refer to it as a "conversion factor". So if size is measured in grams or kilograms and metabolic rate is measured in calories consumed per hour or kilocalories consumed per minute - its not going to matter because "a" is going to convert the values and units in a way that makes sense. Later, you will see that the value of "a" is also going to be related to the shape of the organism.

Another thing to notice about the equation is that when presented in the above simplified version (metabolic rate = a* size), this is really like a simplified version of a line (like Y=mx). In this case, "a" is the parameter that specifies slope - and on a normal axis, slope will affect the steepness of the relationship, but the fact that it is linear means that the relationship scales consistently across all sizes. Therefore, "a" (in this equation) does not specify the scaling relationship (because we are interested in how the relationship changes across sizes!). Do you remember our graph of the four mammals and how the line got less steep at larger sizes? The fact that it got less steep with size could therefore not have been affected by parameter "a". That, it turns out, is the role for parameter "b".

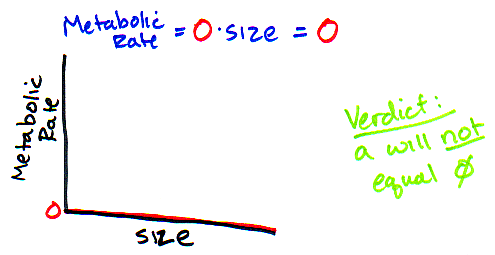
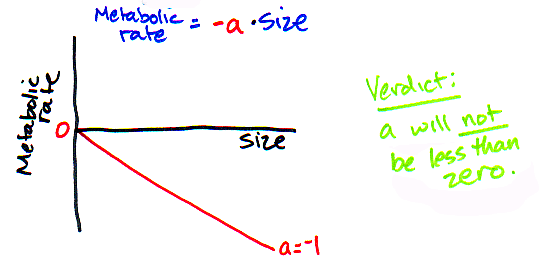
So, "a" is not very informative about the kind of scaling questions we are asking, but it is still worth noting that there are some limits on the range of values that "a" could possibly take. What limits? Well, remember that we know that size is a positive, non-zero number and that metabolic rate must also be a positive, non-zero number. That means that "a" is not going to be equal to 0 or less than 0. Why? If "a" were 0, then metabolic rate is always 0 and we know metabolic rate is never 0! And if "a" were less than 0, then metabolic rate would be negative, and that doesn't make any sense.

AND

So, what values above zero could "a" realistically take on? Because their are so many ways that these relationships could be measured (cal, kcal, gram, kg, etc., etc., etc.) its hard to predict the value that "a" may take (other than being greater than 0), and since it doesn't really mean anything biological anyway, we really aren't going to pay that much attention to this value for the rest of this module (sorry about that, little "a"). Luckily, it turns out that "b" is a much more interesting value - and the one we really care about. We are going to spend A LOT of time thinking about the value of that little "b".