Table of Contents

• Prequiz...
• The Power Function
• 1: Introduction
• 2: What are scaling relationships?
• 3: The power function
• 4: The shape of the power function
• 5: The conversion factor "a"
• 6: The power factor "b"
• Log Transformations
• 7: Introduction
• 8: What are logarithms again?
• 9: Graphing on a log scale
• 10: Visualizing the data
• 11: Getting to a straight line
• 12: The key parameter is "b"
• The value of "b"
• 13: Introduction
• 14: A geometric approach
• 15: Scaling surface area of cubes
• 16: Scaling surface area of cubes
• 17: A "2/3 scaling law"?
• Confronting ideas with data
• 18: Introduction
• 19: An unexpected result
• 20: A "3/4 scaling law"?
• 21: Internal transport systems
• 22: Branching and supply networks
• 23: Deriving the "3/4 scaling law"
• 24: So what's the real value of "b"?
• Review
• 25: Review of Concepts

The origin of the 3/4 scaling law

Although other theories were put forward, it wasn't until 1997, that James Brown (not the singer!), Geoffrey West and Brian Enquist suggested a universal origin of this scaling law. Although their theory is complicated, it is attractive in that it not only explaines the 3/4 power law of metabolism and body size, but also many other body size - physiology scaling patterns that seemed to all be even multiples of 1/4.

For instance, in mammals, life span scales to body weight with a 1/4 power law and heart beats per minute scales to body weight with a negative 1/4 power law. The interesting result of these two opposing values is that, no matter how large a mammal is - mouse or elephant - or how long they live - 1 year or 100 years - all mammals have, on average, the same number of heartbeats over their lifetime. How cool is that!?!

But back to their idea. It is still rooted in the concept that surface area and volume are critical concepts. But this time, instead of the surface area and volume of the entire organism - they focused on the surface area and volume of the networks that transport nutrients and materials throughout an organism's bodies - and are, of course, the machinery of metabolism. Again, the theory is very complex, so as you are reading the next few pages, keep in mind that what we really want you to understand about this theory is the following main ideas:

• The focus is still on geometry, only it is the geometry of internal transport networks
• Brown and his colleagues laid out several important assumptions upon which their theory relies
• Brown and his colleagues used mathematical reasoning (largely through algebraic manipulations) to arrive at the 3/4 power law.

So let's start with the first point, what do they mean by internal transport networks?

These networks include the circulatory system:

and xylem and phloem in plants:

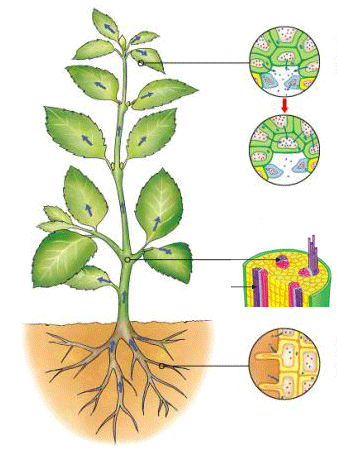
Other examples include the respiratory system and the tracheal system in invertebrates.

Then, they made three critical assumptions about these transport networks. We'll show you those next.