Table of Contents

• Prequiz...
• The Power Function
• 1: Introduction
• 2: What are scaling relationships?
• 3: The power function
• 4: The shape of the power function
• 5: The conversion factor "a"
• 6: The power factor "b"
• Log Transformations
• 7: Introduction
• 8: What are logarithms again?
• 9: Graphing on a log scale
• 10: Visualizing the data
• 11: Getting to a straight line
• 12: The key parameter is "b"
• The value of "b"
• 13: Introduction
• 14: A geometric approach
• 15: Scaling surface area of cubes
• 16: Scaling surface area of cubes
• 17: A "2/3 scaling law"?
• Confronting ideas with data
• 18: Introduction
• 19: An unexpected result
• 20: A "3/4 scaling law"?
• 21: Internal transport systems
• 22: Branching and supply networks
• 23: Deriving the "3/4 scaling law"
• 24: So what's the real value of "b"?
• Review
• 25: Review of Concepts

The scaling of surface area to volume

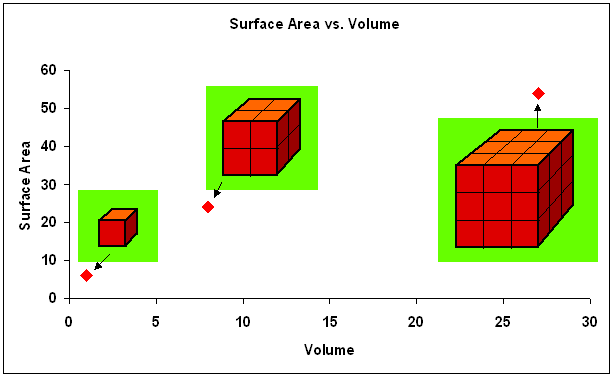
OK, so surface area to volume ratios decrease with increasing size (at least for our cube creatures):

	small cube	medium cube	large cube
length (cm)	1cm	2cm	3cm
surface area (cm2)	6	24	54
volume (cm3)	1	8	27
surface area/volume ratio	6	3	2

To figure out how surface area scales to volume, we use our same, familiar power function:

Y = aX^b only this time, our specific equation is:

Surface Area = a* Volume ^b

Then we plot the relationship:

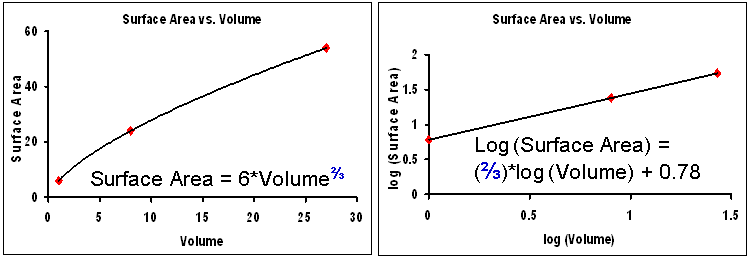
To determine the values of "a" and "b", we "fit" the data to our equations:

(we're not going to go into the mathematics right now of how these equations are "fit", but will save that for another module!)

We went ahead and fit the functions for both the normal and log-transformed data - and you can see that the computed value for the parameter "b" is the same for both!

Power function	Log-transformed function
Y = aXb	log(Y) = b*log(X) + log(a)

COOL! Surface area scales to volume to the ⅔ power!