The branching of the supply network
So, here we are going to present some of the formulas that Brown et al. use to formalize their ideas (though we won't show you how they came up with each individual value) - and we'll show you how manipulating the equations allows you to independently predict that the value of "b" should be 3/4 for the size-metabolism relationship.
If you are having trouble remembering your algebraic rules of equation manipulation - don't worry about it too much - we just want to show how the rules you learned about in math class are actually used in scientific reasoning (so try not to get too caught up in the details!).
So it makes perfect sense that the main supplying branch of an organism's transport network is going to be larger in larger organisms (while the capillaries of elephants and mice are the same size, the aorta of an elephant is going to be much larger than that of a mouse - in fact, a mouse could fit inside an elephant's aorta!). But a critical idea from the Brown et al. model, is the amount of decrease in both the radius and length of each branch is similar between organisms. That means that it is also true that there are going to be many more branchings going from the aorta of an elephant to its capillaries, compared to the number of branchings going from the aorta of a mouse to its capillaries.
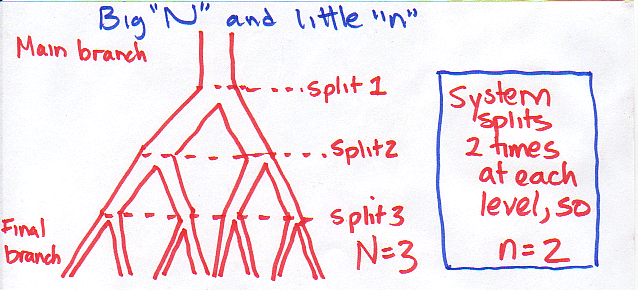
According to Brown et al. - it is more useful to think of the number of times the network branches (rather than the size of the main supplying branch), a value that they call big "N". They point out that this value "N", is going to be related to the size of an organism (this makes sense, the bigger an organism is, the more branching levels it will need). However, big "N" is also related to the number of times the network splits at each level (a value they call little "n"). This also makes sense, because the more times the network splits at each level, the more quickly you get to the smallest branch size.
Brown et al. also recognize that this relationship may not scale linearly, so they added a scaling parameter (b). So, based on this reasoning, they formalized the relationship mathematically with the following equation:
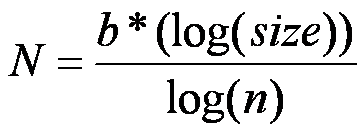
And just to remind you:
N = the total number of times the transport network branches from the top level (i.e., aorta) to the final level (i.e., capillary),
b = the scaling parameter, and
n = the number of times the network splits at each level (so each branch splits a consistent number of times (i.e., 2) as it moves down each level).
Of course - we are interested in the value of "b" - so, let's solve for "b"? How do we do that? We cross-multiply, of course!
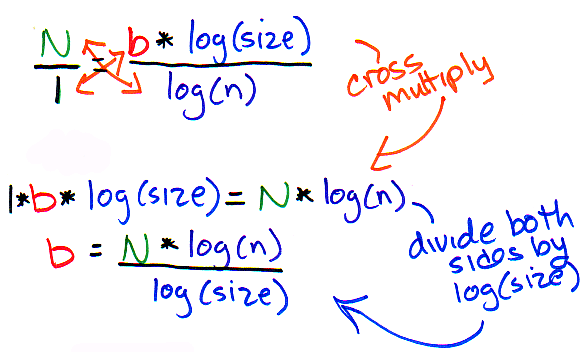
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu