Table of Contents

• Prequiz...
• Part I Two Opposing Gradients
• 1: Getting through membranes
• 2: Going with the flow
• 3: Permeability is key!
• 4: Meet the neighborhood
• 5: Getting groovy with gradients
• 6: Some real numbers...
• Part II Two Useful Equations
• 7: The Goldman Equation
• 8: Playing with the Goldman Equation
• 9: The Nernst Equation
• 10: Taking Nernst for a test drive
• 11: More about Nernst
• 12: How about those logs?
• 13: Pumps and channels
• Part III The Action Potential
• 14: At equiliubrium? Or far from it?
• 15: Opening the gate
• 16: The action potential and the Goldman equation
• 17: Action potential and the Nernst equation
• Part IV Review
• 18: Summary

 

Summary

Ions can only pass across the cell membrane by means of channels (NET movement DOWN a gradient) or energy-driven pumps (NET movement AGAINST a gradient).

The flow of ions across a membrane is determined by the concentration gradient and the voltage gradient. The cell membrane is only permeable to some ions – channels are usually open only for potassium ions, so K⁺ will leak out of the cell leaving a slight negative charge inside. This creates the voltage gradient, which makes K⁺ ions come back into the cell until equilibrium is reached, i.e. the voltage difference balances diffusion.

The equilibrium membrane potential is determined by the concentrations of all the relevant ions inside and outside the cells, and their permeabilities. The Goldman equation takes account of all ions while the Nernst equation allows you to calculate the membrane potential for individual ions assuming that the membrane is permeable only to that ion.

The membrane potential is closest to the equilibrium potential for K⁺ which can be determined by the Nernst equation. In its simplified form the Nernst equation is:

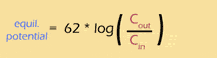
Unlike K⁺, sodium ions are kept out of equilibrium by gated sodium channels. When these channels are opened Na⁺ rushes into the cell down both concentration and electrical gradients. This results in depolarisation. Voltage-gated potassium channels then open resulting in hyperpolarisation and re-establishment of equilibrium once the action potential has passed.

Learning Outcomes

 

Having completed this module, you should now be able to:

• Predict how ions will move across a membrane according to their permeability and the electrochemical gradient (concentration gradient plus voltage gradient).
• Calculate the equilibrium membrane potential for each ion using the Nernst equation.
• Use the Goldman equation to predict the membrane potential during an action potential.

If you want a printer-friendly version of this module, you can find it here in a Microsoft Word document. This printer-friendly version should be used only to review, as it does not contain any of the interactive material, and only a skeletal version of problems solved in the module.