MathBench > Cellular Processes

Diffusion through a Membrane



In the same way, a continuous equation constantly "checks" its variables to see which direction it should be heading (on a graph, rather than a road). A discrete equation only checks every once in a while, every Δt to be specific.

Here is a graph of the solution to the continuous model:

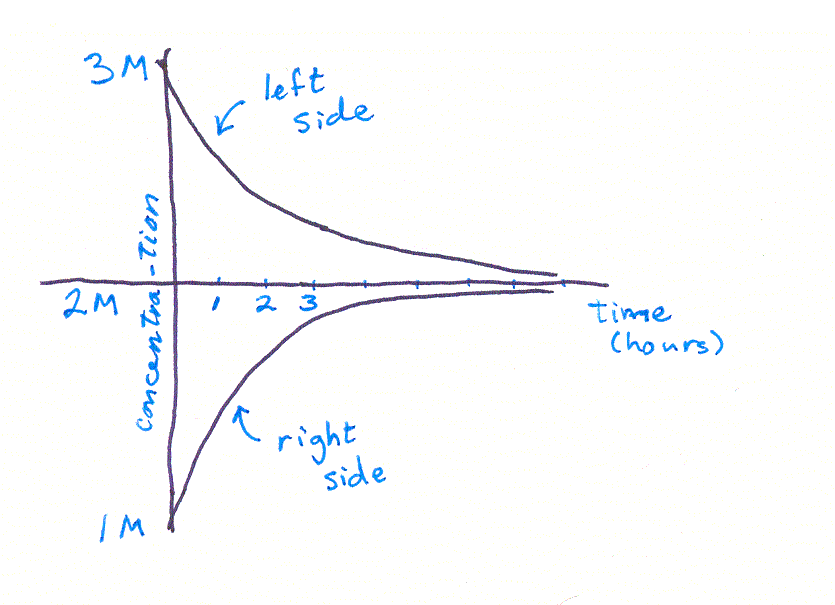
This graph shows the concentration of particles on the left and right sides of a membrane. At the beginning there are way more particles on the left, so the curves are far apart. Towards the end of the time, the compartments have a similar number of particles, so the curves are close together.

As we've said before, how fast the particles change places depends on how different the two compartments are, in other words, how far apart the two curves are. When the curves are far apart, the rate of change is fast and the curves are steep.

And, since we are graphing a solution to the CONTINUOUS equation, it is as if, at each miniscule timestep, we recalculate the concentrations in each compartment and readjust the slope. So the curves are nice and smooth.