Table of Contents

• Developing the Equations
• 1: Review of diffusion equations
• 2: The two-compartment model
• 3: What does continuous mean?
• 4: Examples of permeability
• 5: A formula for permeability
• 6: The area of the membrane
• 7: The final equations
• Examples
• 8: Calculating molecular weight
• 9: Molarity of sugar-goo
• 10: Practicing conversions
• 11: Rate of flux
• 12: Review
• Discrete vs. Continuous
• 13: A metaphor
• 14: Continuous curves
• 15: Discrete curves
• 16: Iterating the discrete curve

continuous form: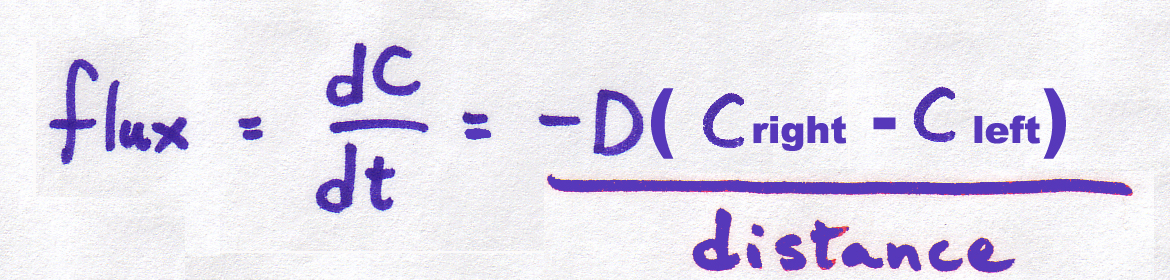
discrete form: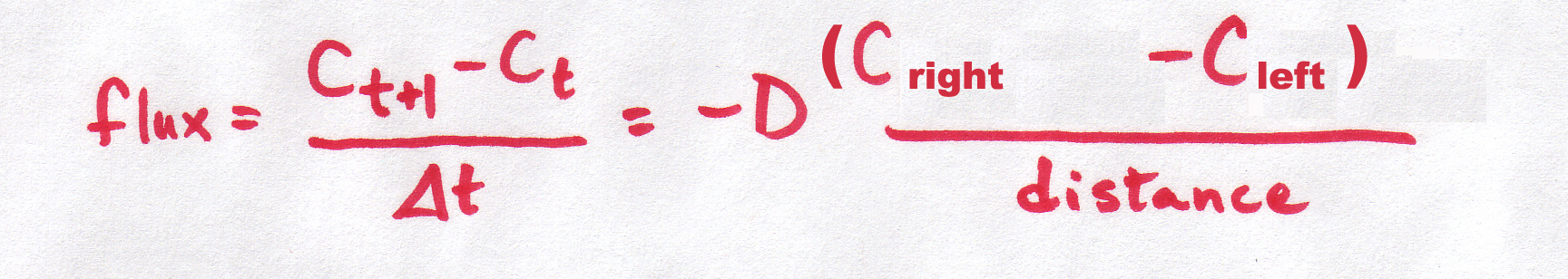

Notice that we replaced the "position+1" and "position" subscripts with "right" and "left", but we haven't changed anything else (yet).

First, SO WHAT DOES CONTINUOUS MEAN ANYWAY?

The old "continuous" equation was continuous over both space (the positions in the tube idea) and time (the rate of diffusion changed gradually).

The new continuous equation will be continuous in time only. It is not continuous in space because we now have only two compartments.

The "discrete" equation is even easier -- it is not continuous in space (remember the 2-compartment model) OR time (the rate of diffusion stays the same for whatever time interval you specify). For example, if you use the discrete equation with 1 second timesteps, the rate only gets recalculated every second, and the graph looks "blocky". This is OK because the rate isn't changing very fast. If it was, the discrete equations which only calculate the rate every one second, might seriously mis-estimate the situation.

We'll continue to develop the equations in both continuous and discrete form, and at the very end of the module, we'll compare their performance.