MathBench > Cellular Processes

Diffusion through a Membrane

Getting personal with P

What is this new measure P is and how does it relate to what we had before????

We want to know how much of our sugar is crossing the proverbial border and going into the other side of the membrane. So permeability (P) is going to depend upon 3 things:

1. P depends in part on D (the diffusion coefficient), which is determined by the size of the particle diffusing and the solution being diffused through. All else being equal, particles with a higher diffusion coefficient also have a higher permeability.

--> P increases when D increases.

2. P also depends on the thickness of the membrane. All else being equal, permeability is higher when the membrane is thinner. (Thus P takes care of the dx or Δx that was in the old diffusion equation).

--> P decreases when Δx increases.

3. Finally, there is a term we can measure and come up with experimentally, called K. Molecules that are "slippery", like lipids, have a high value of K, while charged particles (like the ions from salt) have a low value of K. And K can vary over a huge range, much more so than either P or Δx or D.

--> P increases when K increases.

So now we have a new measurement which is important for diffusion through a membrane P which is.....

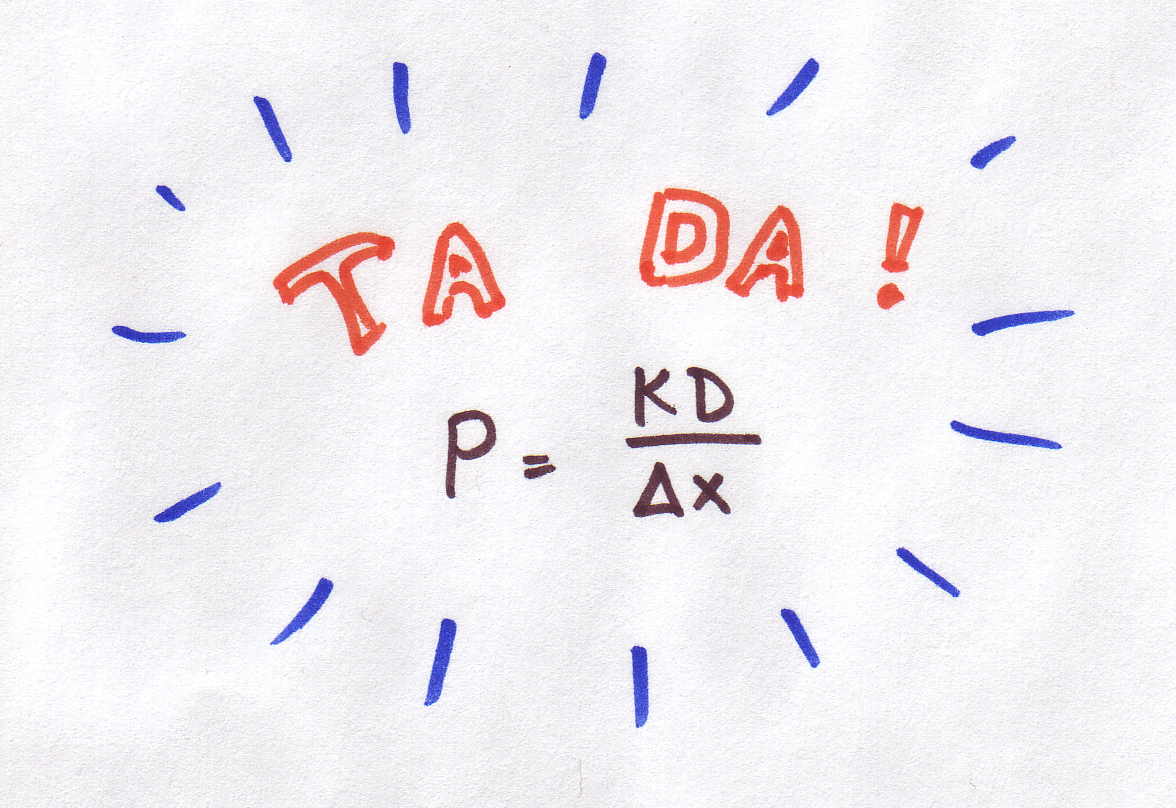
This is the important quantity which will now stand in for just plain old D in our diffusion equations above. (The units of P, in case you have an inquisitive mind, are cm/s).

Assume that the diffusion coefficient (D) is 1 x 10-6 cm2/sec at 10oC, and that the membrane is 1 mm wide (0.1 cm),K=0.004. What is P equal to?

(To make this problem interactive, turn on javascript!)

I think I have the answer: P = 4 * 10-8 cm/sec

In nature, the permeability constant is normally very small, usually around 0.00005, although it can be as high as 4. Notice that its important that you get all the units to match before you do the calculations. For example, if we hadn't converted 1 mm to 0.1 cm, the permeabilities would have been 10 times too high.