MathBench > Population Dynamics

Mutation and Equilibrium

>Episode 2: Hardy and Weinberg to the rescue

Exact probabilities

Scribbling in the margin of his book, the Assistant soon had the answer his supervisor was waiting for. His reasoning went something like this...

 

For a given, single locus:

Using p and q, we can formalize the calculations you made a few pages ago. Remember the laws of AND and OR? Here are the same formulas, but when you roll the mouse over the graphics, you'll see the notation with p and q instead of numbers.

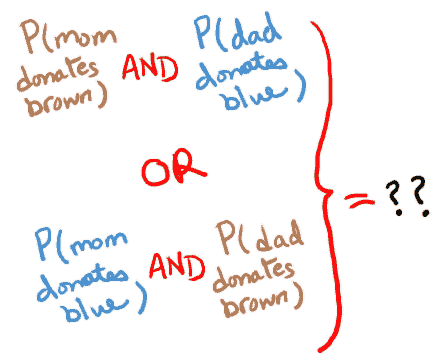
First, what is the probability that an offspring gets 2 blue alleles? (mouse over these images for the answers!)

And the probability that the offspring will be all-brown (no blue allele)?

And finally, the probability that the offspring will be a blue carrier?

DESC

So to summarize, assuming the random mating occurs

"Neat-o" muttered the Assistant with self-aware irony. "Using p and q, I can avoid all the gobbledy-gook about probability. I just need to remember p2 for the dominant genotype, 2pq for the carriers, and q2 for the recessive type. Pretty simple. I bet if I tried, I could even forget where it came from..."

But first, the Assistant shot off a triumphant email to the ME:



Fill in the blanks (you may need a calculator)

Turn on javascript to make this element interactive!


Sir: if 22% of the allele pool is the recessive gene
( in other words, p = and q = ), then, with 2 decimal places,

In other words, rounded to no decimal places, I predict the following distribution:
% / % / % .

p.s., Did you know Google can be used as a calculator? Just type your equation with a equals sign,
i.e., .22 * .22 =, in the search box. Neat-o.

answers:0.78, 0.22, 34.32, 4.84, 61, 34, 5