Viral growth
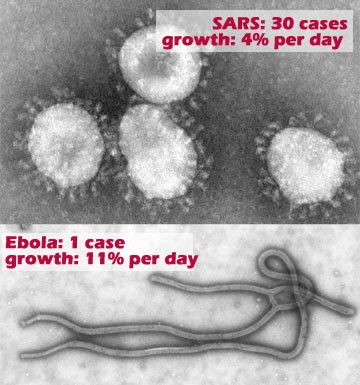 A virus will typically spread exponentially at first if there is no immunization available. Each infected person can infect multiple new people. SARS (Severe Acute Respiratory Syndrome) and Ebola are two such viruses whose impact to affected areas can be devastating. Knowing the rate at which they typically spread is important when you are trying to contain and treat an outbreak.
A virus will typically spread exponentially at first if there is no immunization available. Each infected person can infect multiple new people. SARS (Severe Acute Respiratory Syndrome) and Ebola are two such viruses whose impact to affected areas can be devastating. Knowing the rate at which they typically spread is important when you are trying to contain and treat an outbreak.
Suppose you are working at an international aid organization and there are simultaneous outbreaks of SARS and Ebola. Your organization has only enough resources to travel to and help in one location. Do you rush to help the SARS infected community or the Ebola?
There have been 30 cases reported in the SARS outbreak so far and SARS has an infection rate of 4% per day. Ebola, meanwhile, has only been reported in one person. The infection rate for Ebola is 11% per day. How many people will become infected with each after 15 days?
(To make this problem interactive, turn on javascript!)
- I need a hint: What are the multipliers for SARS and Ebola?
- ... another hint ... : You already know the exponent will be 15 days
- ... another hint ... : You will start with 30 in the SARS equation and 1 in the Ebola equation
I think I have the answer: SARS: 30×1.0415 = 54 and Ebola: 1×1.1115 = 5
If you think you know which community to help, consider the number of people infected after 30 days.
(To make this problem interactive, turn on javascript!)
- I need a hint: Only the exponent changes
I think I have the answer: SARS: 30×1.0430 = 97 and Ebola: 1×1.1130 = 23
One last thing to consider before jumping on a plane; if the infection rate peaks at 60 days and then fizzles out, how many people will be infected at the peak in each community?
(To make this problem interactive, turn on javascript!)
- I need a hint: Still just the exponents
I think I have the answer: SARS: 30×1.0460 = 316 and Ebola: 1×1.1160 = 524
Although there are many fewer cases of Ebola than SARS at the start of the outbreaks, the different growth rates means that the Ebola victims eventually outnumber the SARS victims. How many days before this happens? It's possible to solve this mathematically, but you can also just look at a graph:
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu