Growth of the computer industry
When the home computer first came on the market in the late 1970's there were many people who pooh-poohed the idea. "Why would anyone possibly want a computer in their home?" Boy, were they wrong (and possibly a little embarrassed)! By the mid 1990's 1/3 of US homes had a computer.
In 1997, 37% of homes had a computer. If computers expanded by 12% annually, how many homes had them in 2000?
(To make this problem interactive, turn on javascript!)
- I need a hint: Find the multiplier is 1 + 0.12 = 1.12
- ... another hint ... : This is growth over a three year period, so raise the multiplier to the third power
- ... another hint ... : Starting value is 37
I think I have the answer: 37×1.123= 52%
The Internet also had its naysayers, 
but its usage has grown even faster (32% per year). Starting at 18% of homes in 1997, what would you expect in 2000?
(To make this problem interactive, turn on javascript!)
- I need a hint: What's the multiplier?
- ... another hint ... : how many years?
- ... another hint ... : Where did we start?
I think I have the answer: 18×1.323= 41%
If these rates continued, in what year would the percent of homes with Internet be approximately equal to the number of homes with a computer?
(To make this problem interactive, turn on javascript!)
- I need a hint: Keep increasing the number of timesteps and recalculate
- ... the next calculation... : 37×1.124 vs 18×1.324
- ... another hint ... : Answer will be approximate
I think I have the answer: Sometime between 2001 and 2002
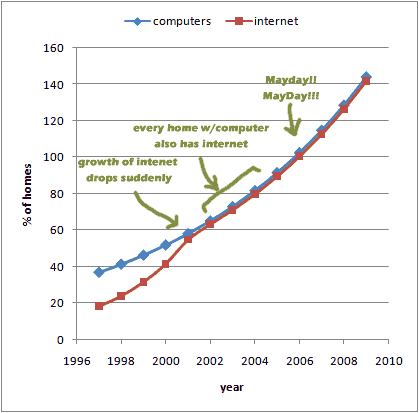
By the way, if you're a bit disturbed by the last calculation, you have a right to be. 
Why? Because the percentage of homes with Internet should not really be able to exceed the percentage of homes with a computer. So if the above model is correct, then
- at the moment when % of homes with computers first equalled % of homes with Internet, the growth of Internet must have slowed to be no more than the growth of computers, and
- after 2002, every home with a computer also had Internet, which we know is not true (like my great aunt Jeanene in Michigan, who uses her Tandy to play mah-jong), and
- in 2006, the number of homes with computer and Internet exceeded 100% for the first time in human history (alert the Onion!)
These three unlikely conditions are shown in the graph below. So is exponential growth "wrong"? Well, the model itself isn't wrong, but we may have applied it a bit too eagerly. Assuming the growth rates stay constant over long periods of time doesn't really make sense.
If, instead, we assume that growth rates gradually decline (both for computer ownership and for Internet access) we get more reasonable results -- which you can see by rolling your mouse over the graph. This is still exponential growth, but the growth rate is no longer constant -- that's why the lines don't curve up.
The moral of the story? Math is fun and all, but don't throw out your common sense.
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu