Table of Contents

• Prequiz...
• Developing the Equations
• 1: Review of diffusion equations
• 2: The two-compartment model
• 3: What does continuous mean?
• 4: Examples of permeability
• 5: A formula for permeability
• 6: The area of the membrane
• 7: The final equations
• Examples
• 8: Rate of flux
• Discrete vs. Continuous
• 9: A metaphor
• 10: Continuous curves
• 11: Discrete curves
• 12: Iterating the discrete curve
• Review
• 13: Summary

Thinking about permeability

So far, we've changed the equations to account for the left and the right side of the model, but we still haven't thought about what's in between -- the membrane. Right now, there's a "diffusion coefficient" (D) in there, but what we need is a number to characterise the membrane.

How much solution will flow through the membrane depends on how permeable the membrane is. Some membranes are very leaky, some only let through certain molecules, and some let through virtually nothing.

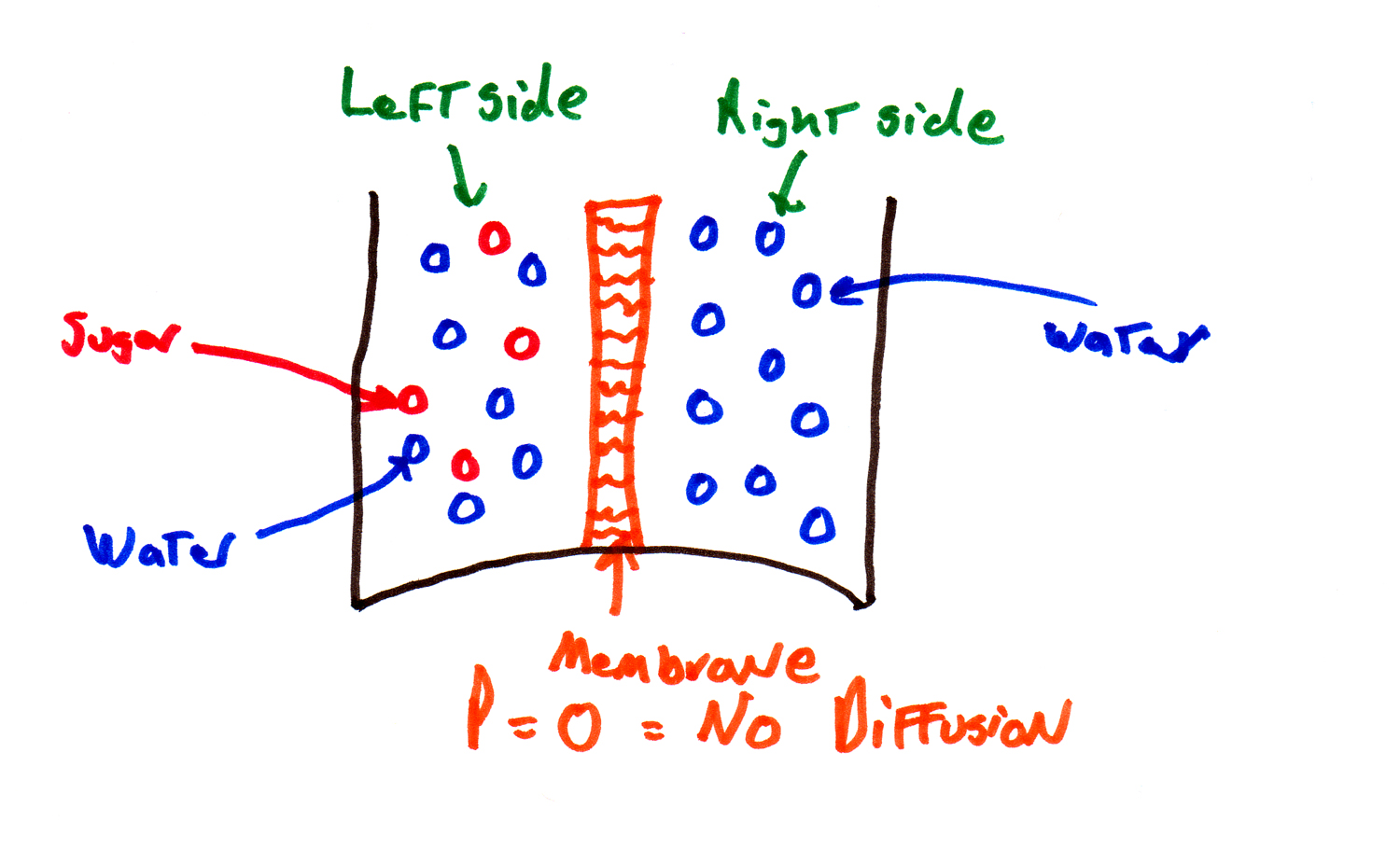
For instance if the membrane was made of cling wrap, it would block all diffusion -- cling wrap is not permeable:

	<--------------- Membrane is totally impermeable to anything ------------->

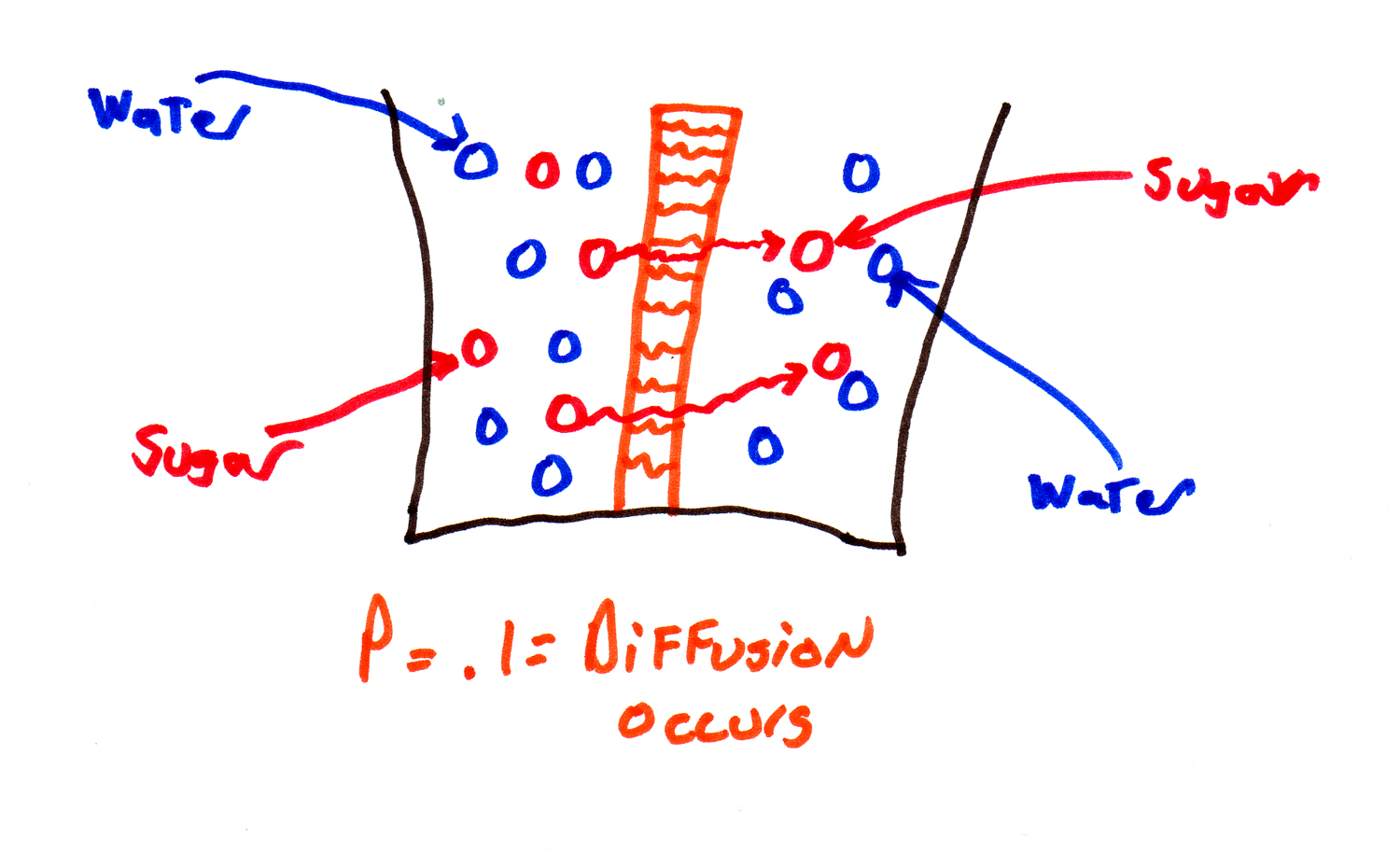
If the membrane was made of window screening, it wouldn't block anything – it's completely permeable.

	<------------ Membrane is completely permeable ---------->

Presumably you could find some substance that was midway between cling wrap and window screening -- something that was partially permeable. This suggests that with a small adaptation, we could continue to use our old diffusion equations (mathematicians LOVE recycling their equations). We could change the diffusion coefficient D into something that accounts for the permeability of the membrane. Let's call that .... P (easy to remember).