The log-transformed power function is a straight line
Why is it that when you log-transform a power function, you get a straight line? To show you, let's remember one of the most fundamental rules of algebra: you can do anything you want to one side of an equation - as long as you do the exact same thing to the other side (We just LOVE that rule!). So, what are we going to do?? Take the log of both sides of our equation:
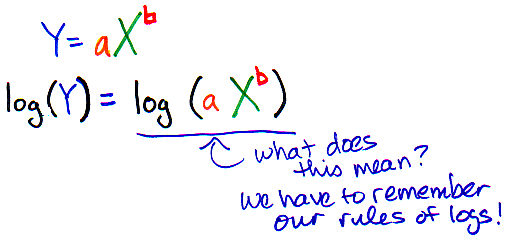
What were those rules of logs again? There are three, but the two that apply to this situation are:
log rule #1: log(a*b) = log(a) + log(b)
log rule #2: log(ab) = b*log(a)
OK, we know you are dying to remember log rule #3, so here it is: log (a/b) = log (a) - log (b) (but you don't need it here)
Lets first apply log rule#1 to our equation:
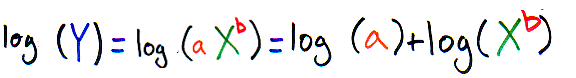
Now, lets apply log rule#2 to our equation:
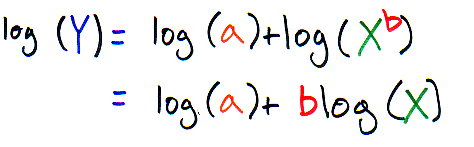
Now, for fun, I'm going to switch around the equation, just a bit - and now it looks just like the equation of a straight line:
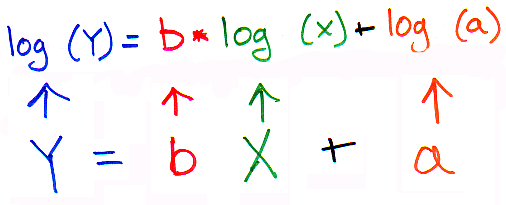
Of course Y = bX + a is just like Y = mX + b (with different letters for the parameters) - and just like we promised - the log-transformed power function (Y=aXb) becomes a straight line (Y=bX + a). It turns out this is a real advantage - because not only is it easier to visualize the data, but it is MUCH easier to work with linear vs. non-linear functions when doing statistical analyses. You'll just have to take our word on that one. So, we're very happy that now we are working with a linear function - but how does this affect the meaning of our parameters we just spent all that time figuring out?
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu