Table of Contents

• Prequiz...
• The Power Function
• 1: Introduction
• 2: What are scaling relationships?
• 3: The power function
• 4: The shape of the power function
• 5: The conversion factor "a"
• 6: The power factor "b"
• Log Transformations
• 7: Introduction
• 8: What are logarithms again?
• 9: Graphing on a log scale
• 10: Visualizing the data
• 11: Getting to a straight line
• 12: The key parameter is "b"
• The value of "b"
• 13: Introduction
• 14: A geometric approach
• 15: Scaling surface area of cubes
• 16: Scaling surface area of cubes
• 17: A "2/3 scaling law"?
• Confronting ideas with data
• 18: Introduction
• 19: An unexpected result
• 20: A "3/4 scaling law"?
• 21: Internal transport systems
• 22: Branching and supply networks
• 23: Deriving the "3/4 scaling law"
• 24: So what's the real value of "b"?
• Review
• 25: Review of Concepts

Three assumptions about internal transport systems

Brown et al. (our fancy, scientific way of saying Brown and his colleagues) first outline three fundamental assumptions that underlie their theory. Almost all theories have basic assumptions that scientists detail and hope you will accept. It is always our job as critical thinkers to examine the assumptions of someone's theory. If we don't buy the assumptions, we may want to reject the theory (but then again, we may not).

So, the first three fundamental assumptions of Brown et al.'s theory:

1) Organisms have evolved to minimize the energy necessary to transport materials throughout their bodies.

OK - that makes perfectly good sense!

2) In order to supply the entire volume of an organism, it is necessary to have a network of tubes in a hierarchical branching pattern, and they claim that the branching pattern is a self-similar fractal.

Whoaa - what the heck does that mean???

Let's start with the idea of a network of tubes that branches in a hierarchical fashion. Think about it in terms of the circulatory system - the first, largest branch is the aorta - then that splits into several smaller branches, each of which splits into several smaller branches - and each of those splits into several smaller branches - and so on, and so on, and so on - until you reach the final branching level - the capillaries!

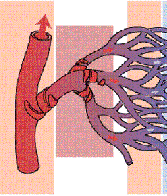
These capillaries have to supply every last millimeter of tissue in each organism. So, as you can imagine, there are a lot of branches - and those capillaries reach out and fill the entire volume of the organism (so of course the branching pattern is much more complex than that shown above).

So, what does it mean that the network is a self-similar fractal? In this case, it means that every time the system branches - it branches an equal number of times. So if the aorta branches four times, then each of those branches will branch four times - then each of those branches will branch four times, and so on, and so on, until you get to the final level - the capillaries (so the picture above does not show a self-similar branching pattern).

And their final, basic assumption:

3) That the final branch of the network, where nutrients and materials are actually exchanged is size-invariant.

So, what does that mean?

Again, this is easiest to think of in terms of the blood circulatory system. For that case, it means that no matter how big an organism gets, that their capillary size is the same. This actually makes a lot of sense - because what limits the size of capillaries (and other material transport systems like lungs and trachea and xylem)? The limits of diffusion, of course! The materials must be able to diffuse efficiently - and as soon as the size of the tube becomes too large, diffusion is no longer efficient. Diffusion is going to occur at the same rate across all organisms! So, the largest allowable size of the capillaries is going to be the same, whether you're a mouse or a moose or an elephant or a whale! If the idea of the limits of diffusion doesn't sound at all familiar - please revisit our diffusion module that is still available for your reading pleasure!

So, what do you think? Do you believe their assumptions? If so, great! If not, let's keep following their argument anyway.

It is beyond the scope of this module to detail all their reasoning - but their theory is related in a more complex way to many of the concepts of volume and area that we covered earlier and how the ratios of these quantities are conserved from branch level to branch level. Although we won't detail the derivation of these relationships, we will show you how manipulating the equations they developed allowed them to arrive at their final conclusion: that the scaling exponent, "b", should be equal to 3/4.