Table of Contents

• Prequiz...
• The Power Function
• 1: Introduction
• 2: What are scaling relationships?
• 3: The power function
• 4: The shape of the power function
• 5: The conversion factor "a"
• 6: The power factor "b"
• Log Transformations
• 7: Introduction
• 8: What are logarithms again?
• 9: Graphing on a log scale
• 10: Visualizing the data
• 11: Getting to a straight line
• 12: The key parameter is "b"
• The value of "b"
• 13: Introduction
• 14: A geometric approach
• 15: Scaling surface area of cubes
• 16: Scaling surface area of cubes
• 17: A "2/3 scaling law"?
• Confronting ideas with data
• 18: Introduction
• 19: An unexpected result
• 20: A "3/4 scaling law"?
• 21: Internal transport systems
• 22: Branching and supply networks
• 23: Deriving the "3/4 scaling law"
• 24: So what's the real value of "b"?
• Review
• 25: Review of Concepts

A geometric approach to a biological problem

All the way back to the 1800's, people suspected that the scaling of size and metabolism is going to be related to the amount of heat loss experienced by an organism (since all organisms require heat to carry out their metabolic processes) and therefore metabolic rate is going to be related to how organisms lose heat as they get larger.

So now we are interested in two quantities, size and heat loss, both of which can be related to geometry.

The first we've already talked about - size. Of course, there are many ways to measure size, but in scaling studies weight is the most common because it captures size increases in all three dimensions. For instance, if we used only height to measure increases in size, then we may not be taking into account organisms that get bigger by getting wider. Weight is directly related to volume, and volume captures growth in all three dimensions. So, for size, we are interested in volumetric growth.

What about heat loss? How do organisms lose heat? Where do you lose heat? Through your skin of course! Since your skin covers the surface of your body, this becomes an issue of surface area, another geometric concept. So, in order to come up with a specific prediction of how size may scale with metabolic rate (if this relationship is driven by heat loss), we need to determine how surface area scales with volume.

The critical question is, if you double or triple the linear dimensions of an object, do you double (or triple) its surface area and volume also? Would the ratios of volume to surface area or volume to length remain constant? Lets start by imagining a very simple organism that is shaped like a cube. As these cube-like organisms became larger, how much surface area (skin) would they have relative to their total body size?

To answer these questions, imagine that you could build the three cubes illustrated below using sugar cubes 1 cm on a side. The first figure is a single sugar cube, the second consists of 8 sugar cubes, and the third is assembled from 27 sugar cubes.

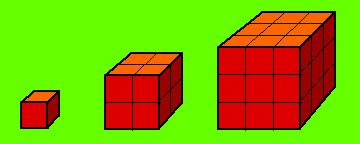
To think about this problem, take out a scrap of paper (and get out your calculator!) - and determine the following quantities:

	small cube	medium cube	large cube
length (cm)	1cm	2cm	3cm
surface area (cm2)
volume (cm3)
surface area/volume ratio

The best way to compute the surface area, is to first determine the surface area of one face of the cube. What is that quantity? You probably remember that area of a square is length². Since each cube has six faces, then the surface area of the entire cube is going to be equal to 6*(length²).

For the volume, just count the number of individual cubes that makes up each of the larger cubes, and remember that the volume of each little cube is 1cm³ (1cm x 1cm x 1cm). After you have filled in the surface area and volume rows, calculate the surface area to volume ratio. What happens to the surface area to volume ratio as the cube gets larger?