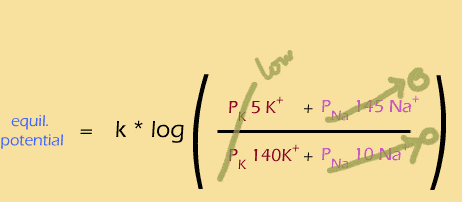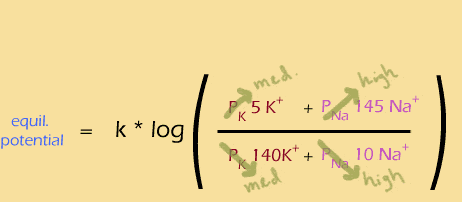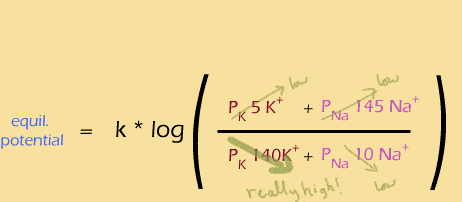MathBench > Cellular Processes

Nernst Potential

 

Action Potential and the Goldman Equation

 

So let's look at the action potential in a little more detail. The first thing that happens is that the gated sodium channels open rapidly, while additional potassium channels also open, but much more slowly. The sodium channels quickly reach a peak and begin to close, while the additional potassium channels lag behind but eventually close as well. Here is one way to visualize that sequence of events:

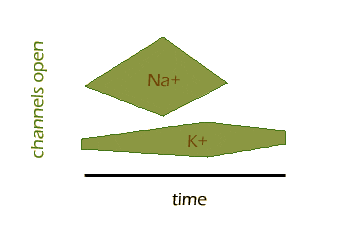
You can see how Na+ channels open and close quickly, while K+ channels take longer. Also, some K+ channels are open before and after the action potential, as we already know.

Can we use the Goldman equation to help predict the membrane potential during an action potential? I'm going to leave out the Cl- terms in the Goldman equation, so we can focus on sodium and potassium.

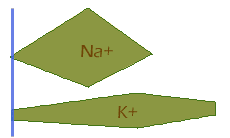
At the beginning of the action potential, only K+ channels are open, so the membrane potential is negative and fairly similar to the Nernst potential of K+ (rollover each of the following equations to see its simplified form):

Then the sodium channels open rapidly, boosting the permeability of sodium, causing depolarization and a positive membrane potential:

2

 

Notice that the actual number of ions inside and outside the cell have hardly changed AT ALL. All this de-, re-, and hyper-polarization will happen solely because the permeabilities are changing (i.e., channels are opening and closing). Relative to the number of ions already inside the cell it only takes a very, very small number of ions to enter or leave and change the membrane potential (look back at page 6 where we showed that a million ions a second is really a very small number).

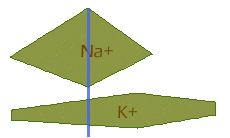
So, next the sodium channels have nearly closed just as the potassium channels reach their peak, looking like this:

2

And finally, the extra potassium channels close, leaving the same situation as in the beginning:

2