Table of Contents

• Prequiz...
• Part I Two Opposing Gradients
• 1: Getting through membranes
• 2: Going with the flow
• 3: Permeability is key!
• 4: Meet the neighborhood
• 5: Getting groovy with gradients
• 6: Some real numbers...
• Part II Two Useful Equations
• 7: The Goldman Equation
• 8: Playing with the Goldman Equation
• 9: The Nernst Equation
• 10: Taking Nernst for a test drive
• 11: The world according to Nernst
• 12: How bout them logs?
• 13: Pumps and channels redux
• Part III The Action Potential
• 14: At equilibrium? Or far from it?
• 15: Opening the gate
• 16: The action potential and the Goldman equation
• 17: Action potential and the Nernst equation

 

The Goldman Equation

Our story so far: The sodium-potassium pump is building up a high concentration of potassium inside your cells, and the cell membranes contain channels which are continually opening and closing, allowing a up to million potassium back out every second. BUT, we know that as potassium leaves, the charge also builds up on the outside of the cell, which ... stops them from leaving. Eventually there is a balance, or steady state, and what we want to know is:

WHERE DOES THAT STEADY STATE HAPPEN?

Another way of saying this is:

WHAT IS THE VOLTAGE DIFFERENCE THAT BALANCES DIFFUSION?

Before I show you the actual equation, let's think about what SHOULD affect the equilibrium voltage difference, or equilibrium potential:

• lots of ions: there are many different ions inside and outside of your cells (usually we talk about K+, Na+, Cl-, and then lump the rest together as anonymous anions, or A-). Each of these ions can (under certain circumstances) affect the diffusion-voltage equilibrium. And they are all operating at the same time, so we should expect to see terms for each in the equation.
• the ratio of concentrations: if I have 1000 times more K+ in the cell compared to outside, that's a very powerful gradient, and it will take a large voltage difference to counteract it, right? Whereas if K+ in the cell is only slightly higher than outside, it won't take much voltage at all. So, I should expect to see the ratio of concentrations in my equation.
• the permeability: remember the brick wall and the screen? If there is no permeability to a given ion, then that ion won't affect the balance. On the other hand, permeability is not an "on of off" kind of thing. Membranes can be slightly permeable, or moderately permeable, or super permeable ... in other words, we should expect to see a variable for permeability in the equation. Even more than that, we know that each ion has its own permeability variable, so we should expect to see lots of ion-specific permeability variables in the equation.

So to summarize, we need the concentrations of all of the relevant ions, both inside and outside the cell, somehow including their permeabilities, and involving a ratio (or fraction) of inside to outside. (This reminds me of a Zits cartoon where Jeremy says he's sure he can write his English paper by morning, since the dictionary contains all the words he needs, and he just needs to put them in the right order...)

And now for the right order... (don't worry, I'll show you how to derive a simpler version of this equation in a few screens, for now let's just take it as a gift)

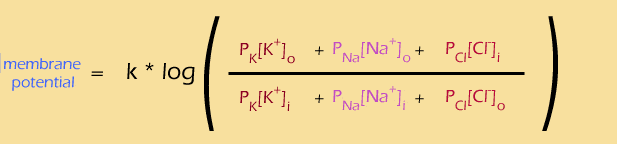
so let's see, we have

• the membrane potential (in electric blue) ... check
• the corresponding concentration gradients (in various shades of red) ...check
• lots of ions (K+, Na+, Cl-) ... check
• permeabitilies of each ion (the P variables) ... check
• ratio of outside to inside concentrations (the fraction) ... check

Looking good so far. There are also a few features we didn't anticipate, such as the constant (k) and the log. We'll talk about them on the next page...