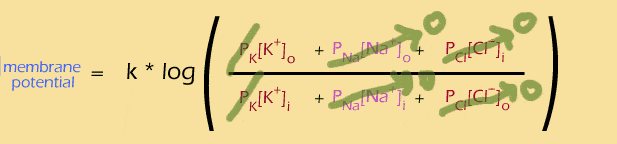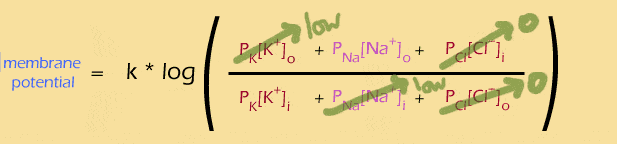Playing around with the Goldman Equation
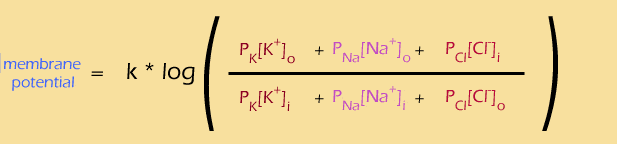
Let's look at the ratio first. This equation is showing you how to combine the effects of all of those different ions... the "outside" ions are on the top of the ratio. You multiply the concentration of each ion by its permeability, then add them all together. So, you can think of the contribution of each ion like this:
| P = 0 | low P | high P | |
|---|---|---|---|
| [ ] = 0 | 0 | 0 | 0 |
| low [ ] | 0 | low | medium |
| high [ ] | 0 | medium | high |
And the equation suggests how to think about all of the different ions -- add up the effects of what's on the outside, and divide by the effects of what's on the inside.
(If you look closely, you'll see that the Cl- ions are actually reversed -- the "inside" term is on the top and the "outside" term is on the bottom -- this happens because chloride is a negative ion, so it has the reverse effect on the voltage potential.)
You can also see that in some cases, the equation will get vastly simpler. For example, what happens if the membrane is permeable only to one ion (like K+) ? The terms for the other ions disappear (because the permeabilities are zero) and the Pk factors also cancel out, leaving a very simple result:
(rollover the equation with your mouse to see the simplified form) So, if the membrane is only permeable to K+, then the membrane potential would be determined by the concentrations of that ion alone.
Likewise, what if channels for both K+ and Na+ were open? We know that there's a lot of K+ inside the cell, and a lot of Na+ outside the cell, so:
The simplified equation (mouse rollover) is ONLY APPROXIMATE, because the "low" K+ outside and Na+ inside really do matter. But as an approximation, we could say that if the membrane is only permeable to K+ and Na+, then their ratio of these two terms determines the membrane potential. This will become important later, when we talk about action potentials.
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu