Table of Contents

• Prequiz...
• Part I Two Opposing Gradients
• 1: Getting through membranes
• 2: Going with the flow
• 3: Permeability is key!
• 4: Meet the neighborhood
• 5: Getting groovy with gradients
• 6: Some real numbers...
• Part II Two Useful Equations
• 7: The Goldman Equation
• 8: Playing with the Goldman Equation
• 9: The Nernst Equation
• 10: Taking Nernst for a test drive
• 11: The world according to Nernst
• 12: How bout them logs?
• 13: Pumps and channels redux
• Part III The Action Potential
• 14: At equilibrium? Or far from it?
• 15: Opening the gate
• 16: The action potential and the Goldman equation
• 17: Action potential and the Nernst equation

 

How bout them logs?

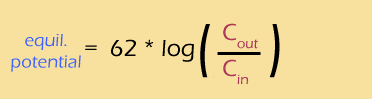
I just can't leave this topic without talking at least a little about logs. Sure, when you're just plugging numbers into an equation, you can (should) ask your calculator to do the logs for you. But if you want to understand how the Nernst potential and the concentration gradients are actually related, you really should understand how that log works.

Multiplying and Adding

Last time we met logs, we were back in the scaling module. A dumb but fairly effective way to remember what logs are is to think of the log as being the length of a log that would be necessary to hold the number, like this:

log size 5 (to hold 5 zeros)	log size 9 (to hold 9 zeros)

 

The important point here is that you only need a slightly bigger log to hold a much bigger number. Put another way, every time you MULTIPLY the number by 10, you only ADD 1 to the log.

So what does this mean for the Nernst potential?

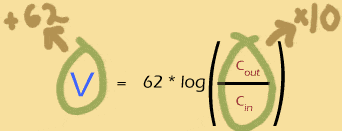
In order to increase the Nernst potential by 62mV, you must multiply the outer concentration of the ion by 10 (or, equivalently, divide the inner concentration by 10).

Take home message: Concentration gradient and Nernst potential are NOT proportional to each other! If you double the outer concentration, you do NOT double the Nernst potential.

and (don't skip this one)...

 

What goes up must come down

If multiplying the concentration gradient by ten adds 62mV to the Nernst potential, then its a good bet that dividing the gradient by 10 will subtract 62mV from the nernst potential. Makes sense:

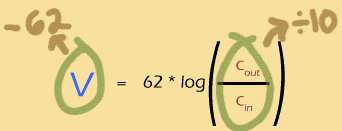
Logs of numbers less than 1

The log of 1 is 0 -- because there are no zeros or other digits after the 1. But what about the logs of measurements smaller than 1? They get a minus sign (to show that the measurement has only decimal places) but the absolute value of the log tells you how many decimal places -- so log(0.001) is -3, but log(0.000000001) is -9.

log size -3 (to hold 3 decimal places)	log size -9 (to hold 9 decimal places)

 

So when will we be taking the log of a number smaller than 1?

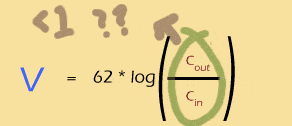
Whenever C_in is bigger than C_out, the log will be negative.

Whenever C_out is bigger than C_in, the log will be positive.

If the two are exactly equal, the log will be 0 and so will the Nernst potential.

The bigger the imbalance, the bigger the Nernst potential (either + or -).

So you can see that the log of a ratio is just about perfect for thinking about the ins and outs of a system like this.