Table of Contents

• Prequiz...
• 1: Logs of graphs and Graphs of logs
• 2: Method 1: Log, then graph
• 3: The curvy line turned into a straight line!
• 4: To transform or not to transform?
• 5: Method 2: graph, then log
• 6: Graphing bigger (and smaller) numbers
• 7: Try it out
• 8: Just add realism
• 9: Review

Method 1: Log, then graph.

Assuming you have a calculator, it's pretty easy to take the log of each number and then make a graph on normal graph paper. (It might take some time, but that's your problem, right?).

Here's an example. First, just show you the normal graph. No logs involved here. Nothing up my sleeve, either. Before you click on "see the graph", try making a sketch on a scrap of paper....

 

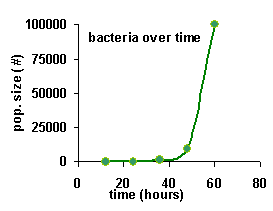
There is problem with this graph -- the y values (number of bacteria) are in the bottom 10% of the graph, except for the very last value. Because the last value is 10 times bigger than any of the other values, the other values all get squished.

But, you should notice something interesting about the data. Every hour, the number of bacteria increases by a factor of 10. That is, the number of bacteria multiply. So, what we need is a multiplicative scale. And that's what logs are. The log tells you how many places the number takes up -- in other words, how many times the number has been multiplied by 10.

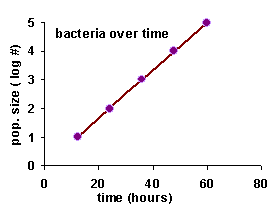
So, let's try the same graph, but take the logs of the data first. If you want to play along at home, you can get out your calculator, calculate the logs, and draw a graph. Otherwise, just click on the button that says "see the graph".