MathBench > Cellular Processes

Nernst Potential

 

The world according to Nernst

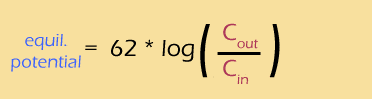
nernst eqation

On the previous page, we found Nernst potentials for the 2 main cations in your cells, and they were quite different:

ion
potential
  
K+
Nernst potential		 -90mV K+
Na+
Nernst potential		 +72mV K+
real cell membrane
resting potential		 -60 to -80 mV K+

And, as you can see from the last line of the table, the Nernst potentials we found for the two ions don't even match the resting potential of a real cell membrane! So what gives?

Actually, what's going on is that the Nernst potential is a kind of idealization -- even a fantasy, if you will -- that is only valid under the two conditions:

  1. The membrane is permeable to the ion under consideration, and
  2. The membrane is NOT permeable to any other ion

We know that membranes are not as simple as this, but in fact the resting potential of most cell membranes is somewhere close to the Nernst potential for K+ ... that suggests that the resting potential is MOSTLY being influenced by K+. And this matches what we know about channels -- in cells at rest, the K+ channels are generally open and others are generally closed.

Simplifying assumptions

In math, the conditions above are known as "simplifying assumptions". There's a reason for making these assumptions -- they make the equations a lot easier to deal with.

The Nernst equation has more simplifying assumptions than the longer Goldman equations. You may have noticed we never actually used the Goldman equation to calculate anything -- in part that is because you need a lot more information in order to use the Goldman equation, including concentrations of all the ions and their permeabilities in meters per second! Getting that information could be quite difficult.

The Nernst equation only requires 2 pieces of information -- the concentration inside and outside the cell. But, it comes up with a rather idealistic answer that doesn't (exactly) fit reality.

Here's a metaphor -- two also fictional characters:

Call the one on the left "sodium" and the one on the right "potassium". If you find you're averaging a loss of $2.50 a day, you know you're listening more to the one on the right !