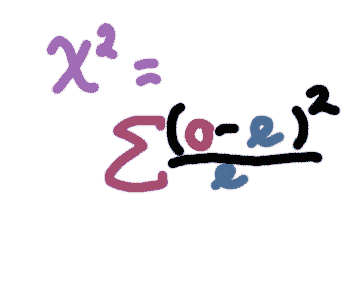One small correction
The method I showed you on the last page was not quite right. For reasons that are difficult to explain without a degree in statistics, you need to SQUARE the raw deviation before dividing by the expected value. So we have the following sequence:
 Determine what you “expected” to see.Find out the difference between the
observed and expected values (subtract) Square those differences Find out how big those squared differences
are compared to what you expected (that is, divide)Add it all up. (This gives a value that we will call a chi-squared statistic. Why "chi-squared" I hear you ask – this is another one of those instances when a degree in Statistics helps!) |
 |
Place mouse on picture for more explanation |
If the final chi-squared statistic is a big number, would this make you think that the data fits the model, or does not fit the model?
(To make this problem interactive, turn on javascript!)
- I need a hint ... : A big chi-square statistic probably means that the individual
numbers you added were also big...
- ...another hint ... : The individual numbers you added were deviations from
the model predictions.
I think I have the answer: Since the individual numbers you added
were deviations from the model predictions, a big chi-squared statistic means
that the data deviate a lot. In other words, the model is a bad fit.
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu