Part III: Exploring the Lineweaver-Burke plot
So far we have a beautiful analysis of the Michaelis-Menten equation, except for one teeny tiny problem. We still don't know how to measure Vmax with any accuracy (remember the budget-busting exercise a few screens back?)

Michaelis and Menten came up with their equation in 1913. This small problem of Vmax was solved by two other guys (named Lineweaver and Burke) in 1934, which I'm sure was a huge relief to everyone. The solution is not very intuitive, but it is elegant.
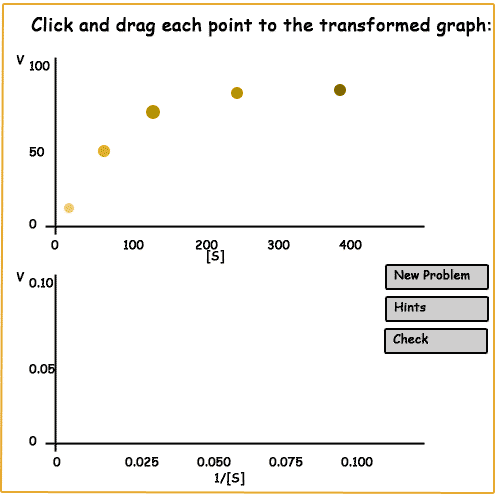
You should be familiar with the idea of log-transformation as a way of "unsquishing" data. The basic insight of Lineweaver and Burke was a different kind of data transformation could help measure Km and especially Vmax more effectively. This transformation is called a "double reciprocal", which means that instead of plotting Vmax against [S], we plot 1/Vmax against 1/[S].
To see how this works, try moving each point in the plot on the left into the correct spot on the transformed plot to the right:
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu