MathBench > Cellular Processes

Diffusion

How many macrophages does it take to kill a virus?

Some organisms move around more or less at random, so we can use diffusion to "model" how these cells move. This works fine, as long as you accept the assumption / simplification that these organisms are mindless little robots that walk around changing directions randomly. Sometimes this is a reasonable concession to make in exchange for the simplicity and power of the diffusion model, other times it is not. It’s a choice that you, the person implementing the model, need to make.

Here is an example of using diffusion to model a cell moving (adapted from Essential Mathematical Biology by N. F. Britton):

The macrophage is a specialized cell that defends that body against foreign materials. Within the lungs, macrophages engulf inhaled viruses and digest them. Macrophages move in a way that is very similar to diffusion – they ooze along at a stately 3 micrometers per minute, but change directions more or less randomly about every 5 minutes.

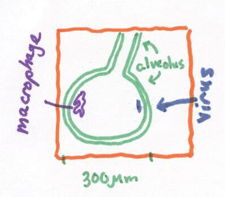
Consider an alveolus (diameter = 300 micrometers) that contains a single macrophage and a single virus. Assume the phage and virus start at opposite ends of the cell and the phage moves in a straight line (not similar to diffusion) towards the virus. How long will it take for the phage to arrive?

(To make this problem interactive, turn on javascript!... may not work in Internet Explorer )

I think I have the answer:

time = total distance / distance per minute = 300 / 3 = 100 minutes

....BUT...(see next page!)