>

MathBench > Cellular Processes

Diffusion

How does flux depend on distance?


Now let's think about Fick's first law in a different way. Before we were interested in the steepness of the gradient as the independent variable (what happens to flux when the gradient gets steeper?). Now we're going to switch gears and think about how flux changes as the distance changes. In other words, we will choose to see distance as the independent variable (isn't this fun? we can make the independent variable anything we want!). To do this, we'll need to use the discreet version of Fick's first law: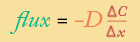

This time, Δx is the independent variable, and the equation is an example of "inverse variation", otherwise known as what happens when you divide by the independent variable, or try to graph something like y = a/x.

 


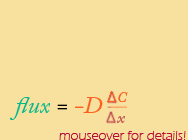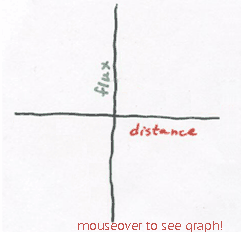If the distance Δx is very small, then the flux is huge. As the distance widens, flux falls off quickly. With a big value of Δx, flux is essentially 0 (although it never quite reaches zero).

So, what does this mean biologically?

An E. coli cell averages about 2 µm in length, while a S. cerevisiae (baker's yeast) cell measures about 9 µm. Assuming the same gradient and D occurs in each cell, how would flux differ?

(To make this problem interactive, turn on javascript!... may not work in Internet Explorer )

I think I have the answer: -D * (ΔC/2) / (-D * ΔC/9) =
9/2, so flux is 4.5 times greater