The gradient in Fick's First Law
Here are our two main points again. If you understand and memorize these two sentences, you will have half of diffusion down cold:
- Diffusion is the net flux of particles down a concentration gradient due to random movement, and
- Diffusive flux is directly proportional to the steepness of the gradient (Fick’s first law).
Let’s make it look more technical. It's easiest to think of a gradient in one dimension (so there is a left and right side). The picture below shows a gradient from left (high) to right (low).
How can we measure this gradient? The easiest thing to do would be to find out the difference between the concentrations on the left and on the right, and the distance between the left and the right. The gradient is the difference between concentrations divided by the distance between the ends:
 |
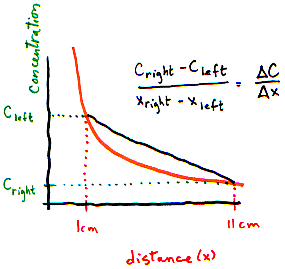 |
What is the left to right gradient? (Use figure above)
(To make this problem interactive, turn on javascript!...also, some elements may work better in Firefox)
- I need a hint ... : On the left, there are 17 particles per 1 cm3 slice. On the
right, there are only 4 particles per 1 cm3 slice.
- ...another hint ... : The distance between the 2 slices is 10 cm.
I think I have the answer: Concentration changes by 13 particles per cm3 per 10 cm distance, or 1.3 particles per cm4.
You could also measure the concentrations closer and closer together to get more exact information. For example you could measure the gradient every centimeter.
 |
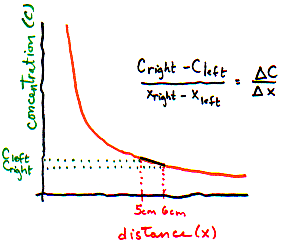 |
What is the left to right gradient? (Use figure above)
(To make this problem interactive, turn on javascript!...also, some elements may work better in Firefox)
- I need a hint ... : On the are 3 particles per 1 mm slice. On the right,
there are only 2 particles per 1 mm slice.
- ...another hint ... : The distance between the 2 slices is 10 mm.
I think I have the answer: Concentration changes by 1 particle per mm3 per 10 mm distance, or 0.1 particles per mm4.
Or every millimeter. Or every micrometer. Here is where calculus comes in handy (yes, Virginia, calculus is actually useful sometimes!). Calculus allows you to calculate infinitely many gradients that are each infinitely short. Instead of taking the difference between concentrations on the left and right side of some distance, we take the difference between concentrations that are infinitely close together, and call it dC. Instead of using some large distance like 1 centimeter or 1 millimeter, we use an infinitely small distance, dx. So the gradient is dC/dx (which, you may recall, is a "derivative" in calculus). dC/dx tells you how much the concentration changes as you move
| We can't directly measure the concentration of particles in infinitely small slices!! But on the graph, we can interpret the gradient as the slope of the line -- which tells us how concentration changes when distance changes very slightly. | |
 |
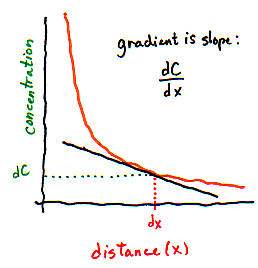 |
We introduce the calculus version of the gradient not to confuse you, but because the flux equation is almost always written in its calculus form, using dC/dx as the gradient. In fact, you can think of dC/dx simply as a single variable that could equally well be called the "gradient".
A note about units:
If you worked through the examples, you saw that the units for the gradient are
particles/length4 (for example: particles/mm4)
These strange units usually throw students for a loop. We all know that mm2 is an area measurement -- in other words, 2-dimensional. And mm3 is a volume measurement, otherwise known as 3-dimensional. So, mm4 sounds like a space-time continuum (the 4th dimension...) but its not anything that fancy. It simply means
the change in particles per volume, over a certain distance.
= change in particles per mm3 per mm1
= change in particles / mm4
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu