Table of Contents

• Prequiz...
• Just Plain Movement
• 1: Measuring Movement
• 2: Directed vs. Undirected Movement
• 3: Measuring Movement Using Flux
• Introducing Gradients
• 4: What is a gradient?
• 5: Watching diffusion happen (applet)
• 6: Visualizing the Gradient
• Fick's Laws, Part I
• 7: Fick's First Law
• 8: The gradient in Fick's First Law
• 9: A familiar equation for Fick's first law
• 10: The diffusion coefficient is the slope
• 11: What are the units for D?
• 12: How does flux depend on distance?
• 13: A fragrant example
• 14: General Transport Equations and Fick's First Law
• Fick's Laws, Part II
• 15: Fick's Second Law ...
• 16: ... is about "time to diffuse"
• 17: A Very Useful Formula
• 18: Time-to-diffuse "explodes"
• 19: General Functions and Diffusion
• Biological Applications
• 20: Biological Applications
• 21: Why do rhinos have lungs and amoebas don't?
• 22: Diffusion is efficient in small organisms, but not big ones
• 23: Diffusion within lungs
• 24: How many macrophages does it take to kill a virus?
• 25: You need a lot of macrophages - or one smart one!
• Review
• 26: Final Review

A familiar equation for Fick's first law

Fick's Law again: Flux is directly proportional to the steepness of the gradient.

So now we know that the gradient is represented by dC/dx, but what does “directly proportional” mean? Hover over the image with your mouse to see how the steepness of the gradient affects the amount of diffusion:

When we have a small gradient, there is not much diffusion going on, but when the gradient is BIG, then diffusion can be substantial. But how can we represent this mathematically? Well, if two quantities are directly proportional, they are related to each other through an equation like y = mx. Hmmm.... this equation should sound familiar -- it's the equation for a line which goes through (0,0).

So, FINALLY, a mathematical equivalent to Fick's law, in both a continuous (calculus) and discrete version. Notice that they both have the same basic form that is directly analogous to the basic equation for a straight line that intersects the origin (y=mx):

Continuous version	Discrete Version

 

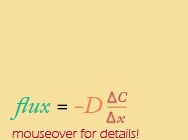So for both equations, "y" is the flux (or more correctly, the flux density), and is dependent (and therefore called the dependent variable) on two quantities: 1) the steepness of the gradient (in red) and 2) a coefficient based on the particular substance being measured (the Diffusion coefficient, "D" - more on that later).

One last note ... Why the negative sign in front of the diffusion coefficient??? Remember that diffusion always goes DOWN the concentration gradient -- its direction is opposite the concentration gradient. So the the diffusion coefficient has a Movement always occurs in a direction OPPOSITE to that of the gradient.