Table of Contents

• Testing differences
• 1: How to convince your boss
• 2: Looking at the data
• 3: Is the average different?
• 4: How big is big?
• 5: How to combine SDs
• 6: Combining SDs for fun and profit
• t-calc and t-crit
• 7: Getting to t-calc
• 8: A formula for t-calc
• 9: Degrees of freedom
• 10: The bottom line (finally)
• Putting it all together
• 11: Give it a try
• 12: Once more for luck
• 13: The big picture

How to combine SDs

Here's what we've got so far:

	n	average	difference	standard deviation (SD)
Fish-2-Whale	8	267 g	94 g	44g
Control	8	173 g		28g

 

We know from the last page that we need to compare the difference in averages (94g) to the standard deviation in some way. But how? We have two different standard deviations (44g for Fish-2-Whale, 28g for the control). Picking just one SD seems like favoritism, so we don't want to do that.

It is tempting to just average the two SDs, but unfortunately the Rules of Statistics have something (slightly) more complicated in store for us. Here is another way of combining the 2 SDs -- it is still not quite correct, but closer:

This way of combining standard deviation looks a lot like the pythagorean theorem, which can help you remember it. However, it has one big flaw: it does not take sample size into account.

And that's a big problem. When you spend do your big experiment with 800 fish instead of 8, you really want all that extra work to count. The 800 fish won't help you if Fish-2-Whale is a failure (remember, statistical tests don't have super-powers), but they will help you if your results fall into a "gray area", where the distributions overlap by a little. That's when you need a large sample size to help you figure out if you're really onto something.

You might object here that sample size is included in the formula for standard deviation, which it is. But that is a bit of an illusion -- you add together 8 deviations, then divide by 7. Or you add together 800 deviations and divide by 799. In other words, the actual sample size doesn't affect standard deviation. In fact, standard deviation does not change in any predicatable way as sample size increases. It stays approximately the same, because it is measuring how variable the population itself is. If the population is highly variable, then SD will be high no matter how many samples you take. If the population has little variability, then SD will be low even if you only take a few samples.

So we need a better way to incorporate sample size. We want the number of Fish-2-Whale fish to affect the Fish-2-Whale SD, and we want the number of control fish to lower the control SD. We'll do this in the simplest way possible:

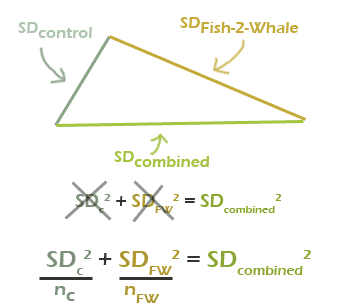
Namely, after we square the SDs, we divide each by its own sample size. Then we add the two values together and take the square root to get the combined standard deviation.