The magic lookup table
Once you know the degrees of freedom (or df), you can use a chi square table, like the one on the right (books sometimes have a more complicated table which we'll talk about at the bottom of the page). Although this table does come from a mathematical function (called a chi-square distribution, go figure!) for our purposes you can basically treat it like it appeared magically. The first thing you need to know is the degrees of freedom in your test. As we talked about on the last page, this is the same as the number of rows in your table minus 1. Use your df to look up the critical value of the chi-square test, also called the chi-square-crit. So for a test with 1 df (degree of freedom), the "critical" value of the chi-square statistic is 3.84. What does critical value mean?
|
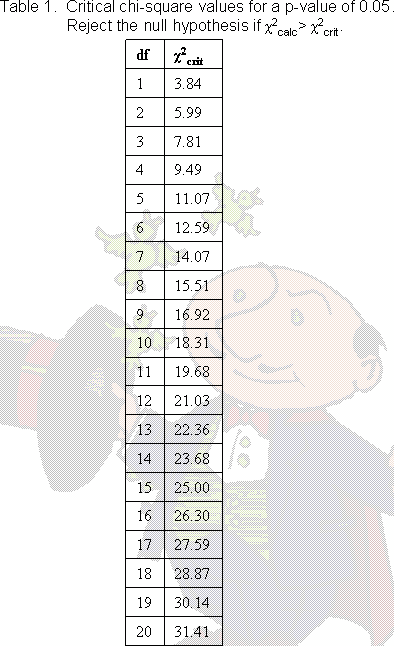 |
Why do you think the chi-square-crit increases as the degrees of freedom increases?
(To make this problem interactive, turn on javascript!)
- I need a hint ... : If you have, say, 15 degrees of freedom,
how many rows are in your table?
- ...another hint ... : For every row in the table you need to calculate another deviation.
I think I have the answer: With a lot of degrees of freedom,
you have a lot of rows in your table. Therefore you're adding
more numbers together to get your final chi-square.
So it makes sense that the critical value also increases.
 Fine print: some tables have many columns, one for each p-value you might be interested in.
In that case, you first need to find the 0.05 p-value (or any other p-value you're asked for), then the
df, then the chi-square-crit.
Fine print: some tables have many columns, one for each p-value you might be interested in.
In that case, you first need to find the 0.05 p-value (or any other p-value you're asked for), then the
df, then the chi-square-crit.
Even finer print: or, you may be asked to find the p-value corresponding to the chi-square-calc. In that case you have to find the right df first, then find the two chi-square-crits that your chi-square-calc falls between, then note the p-value.
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu