And now with coins ...
Why do biology teachers like to talk about flipping coins so much? Sorry, no punchline here -- the reason is that flipping a coin is alot like meiosis.
 |
 |
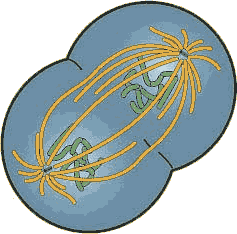 |
What I mean is, when the cell divides to make sperm or eggs, the genetic material also divides. The original cell had 2 copies of each gene (in other words, 2 alleles), but the gamete only gets one. Basically, the original cell could have "flipped a coin" to determine which copy the gamete ended up with. And since this happens in both the mother and the father, its like two coins being flipped and the results tallied.
So with that in mind...
If you flip two coins, what are the chances that both will come up heads?
(To make this problem interactive, turn on javascript!)
- I need a hint ... : P(coin1=heads AND coin2=heads)
- ...another hint ... : This is an AND question, so...
I think I have the answer: 1/4
If you flip two coins, what are the chances that you will get one heads and one tails?
(To make this problem interactive, turn on javascript!)
- I need a hint ... : Be careful!! There are 2 ways this could happen --
first heads then tails, or first tails then heads - ...another hint ... :P((heads AND tails) OR (tails AND heads))
- ...another hint ... :There are 2 ANDs and 1 OR, so you'll need to multiply twice and add once
- ...one last hint?...: (1/2 * 1/2) + (1/2 * 1/2)
I think I have the answer: 1/2

If you flip two coins, what are the chances that you won't get two tails?
(To make this problem interactive, turn on javascript!)
- I need a hint ... : Again, this could happen two ways
- ...another hint ... : tails and tails, or one head and one tail
- ...another hint ... : P(TT) = 1/4 and P(TH or HT)=1/2 (both from the problems above!)
I think I have the answer: 3/4
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu