MathBench > Cellular Processes

Diffusion

Fick's Second Law

Fick’s first law tells us HOW MUCH flux to expect. Fick’s second law gets into more detail, telling us the rate at which concentration is changing at any given point in space. This law takes the form of a “partial differential equation”, that is, an equation that allows us to solve for rates involving both time and space.

If this sounds complicated … it is. We won’t go into how this law works, except to say that when you integrate over time, you get a very useful (and easy to understand) result: a formula for how long diffusion takes over a specified distance:

 

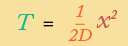Assuming you know a diffusion coefficient, this formula allows you to determine how much time is necessary (on average) for particles moving by diffusion to traverse any given distance

Try it out:

If D = 0.00001 cm2/s (for oxygen through water), how long would it take the oxygen to diffuse 0.01 cm below the surface of a still pond?

(To make this problem interactive, turn on javascript!... may not work in Internet Explorer )

I think I have the answer: (0.01cm)2 / (2 * 0.00001cm2 / sec)) =
5 sec

How about 0.1 cm?

(To make this problem interactive, turn on javascript!... may not work in Internet Explorer )

I think I have the answer: (0.1cm)2 / (2 * 0.00001cm2 / sec)) =
500 sec

What about 1 cm?

(To make this problem interactive, turn on javascript!... may not work in Internet Explorer )

I think I have the answer: (1cm)2 / (2 * 0.00001cm2 / sec)) =
50,000 sec


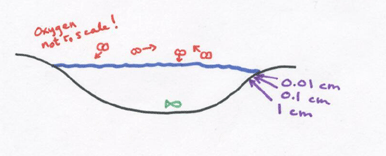
Any fish hanging out at 0.1 cm belong the water surface would die from oxygen debt if they had to rely on diffusion to bring them oxygen – – luckily there are also water currents