Table of Contents

• Prequiz...
• Just Plain Movement
• 1: Measuring Movement
• 2: Directed vs. Undirected Movement
• 3: Measuring Movement Using Flux
• Introducing Gradients
• 4: What is a gradient?
• 5: Watching diffusion happen (applet)
• 6: Visualizing the Gradient
• Fick's Laws, Part I
• 7: Fick's First Law
• 8: The gradient in Fick's First Law
• 9: A familiar equation for Fick's first law
• 10: The diffusion coefficient is the slope
• 11: What are the units for D?
• 12: How does flux depend on distance?
• 13: A fragrant example
• 14: General Transport Equations and Fick's First Law
• Fick's Laws, Part II
• 15: Fick's Second Law ...
• 16: ... is about "time to diffuse"
• 17: A Very Useful Formula
• 18: Time-to-diffuse "explodes"
• 19: General Functions and Diffusion
• Biological Applications
• 20: Biological Applications
• 21: Why do rhinos have lungs and amoebas don't?
• 22: Diffusion is efficient in small organisms, but not big ones
• 23: Diffusion within lungs
• 24: How many macrophages does it take to kill a virus?
• 25: You need a lot of macrophages - or one smart one!
• Review
• 26: Final Review

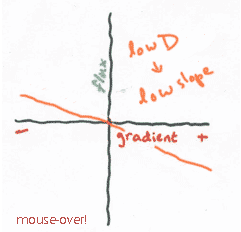
The diffusion coefficient is the slope

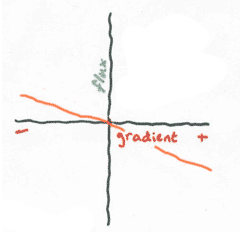
So, we know that the equations describing Fick's First Law are analagous to the general equation for a straight line with a negative slope that intersects the origin (y = -mx), and so you should already have a pretty good idea of what the graph of this function will look like (the calculus version is below, but the discrete version would look exactly the same!).

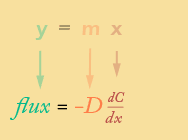In this case, the dependent variable is flux, and the independent variable is the gradient (dC/dx). Remember, dC/dx only looks scary. In reality it just means "the steepness of the gradient".

But what is the biological meaning of the slope of the relationship? Or, put another way, how is the driving force (the gradient) translated into a response (flux)? As we mentioned earlier, the constant in the equation gets its own name, D (called the diffusion coefficient). D is something that needs to be measured, and it’s different for each unique situation (a particular molecule in a particular medium at a particular temperature). For example, the diffusion coefficient of oxygen in water is a consistent value at room temperature, but if you heat up the water, D goes up – the oxygen diffuses faster when the temperature is higher or if you substitute molasses for water, D goes down – oxygen has a hard time diffusing through molasses (and so would you!). If a larger molecule (say, a protein) is diffusing through water, D will again go down again, since big molecules move less and therefore diffuse more slowly than small ones.

So what happens to flux if the diffusion coefficient changes? According to Fick's first law, these quantities are directly proportional to each other (remember the function is like y = mx) and -D is the slope. If you are interested in the diffusion of glucose instead of oxygen, you get a different diffusion coefficient D, and so the line has a different slope. In other words, when D is high, the same gradient causes more diffusion.

So, we've spent a bit of time talking about this diffusion coefficient (D) - but what does that really represent biologically? One way to figure that out is just to look at the units of D to figure out what it is really describing.