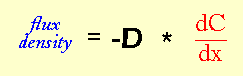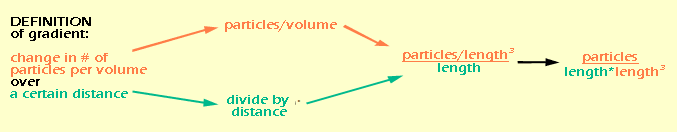What are the units for D?
The diffusion coefficient (D) describes how long it takes a particular substance (like oxygen or proteins, etc.) to move through a particular medium (like water or molasses).
The units of D are length2/time, and usually reported in cm2/sec. Why length2/time? It's possible to show that these are the necessary units using "dimensional analysis", which basically means doing algebra on the units. Dimensional analysis is a general and extremely useful technique if you're trying to come up with mathematical descriptions of how natural systems work.
If you want to see all the gory details, read the box below. Otherwise you'll just have to trust us on this one.
INQUIRING MINDS WANT TO KNOW: It's not intuitively clear what the diffusion coefficient should be measuring. So, one way to figure out the units is through a process called dimensional analysis -- a fancy way of saying, "do algebra on the units". In dimensional analysis, you use the fact that you know that units have to balance out on each side of the equation. We know that we are going to balance the equation of:
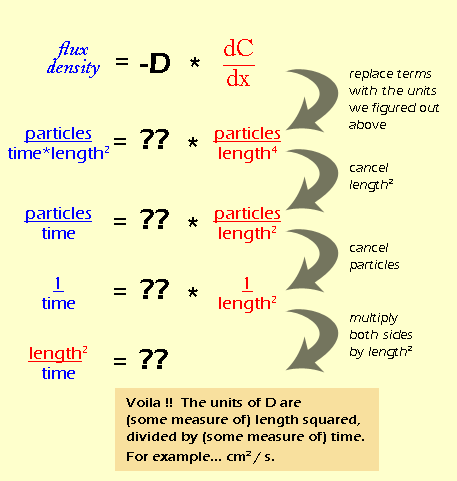
Before we can even think about the units for D are, we need to figure out what the units for flux density are, and also the units for the gradient (dC/dx). Remember that we defined flux density as the net rate at which particles move through a certain area (all the way back on page 3). Let's break this definition down into units:
If you're confused about how "length" suddenly appeared, think about it like this: area is basically a 2-dimensional space, so in a generic way, we can think of it as "length2". And "time" ended up on the bottom of the fraction by the rules of rearranging fractions. So let's do the same thing for the gradient:
Again, distance is a 1-dimensional measure of space, so it is equivalent to "length", while volume is a 3-dimensional measure of space, or "length3". By rearranging the fraction, we see that all of the "lengths" end up on the bottom. It would be easier to write this as "length4", but I wanted to keep the color coding so you could see where they came from. Now that we know the units for flux density and gradient (which really come from the definitions of those quantities) we can figure out the units for D (which we don't have a definition for). We do this essentially by doing algebra on the units.
|
Dimensional analysis on its own is not too hard, but in this example the units for flux density and concentration gradient are pretty tricky. In fact, during the first several drafts of this module, we had the units wrong. Once you know the initial units, though, the rest is just manipulation.
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu