MathBench > Population Dynamics

Mutation and Equilibrium

>Episode 1: The Blue Hair Backstory

Using the laws of AND and OR

Before we start, make sure you are clear on why the line of reasoning below works. Random mating means that each parent will contribute genetic material (to its offspring) which is representative of the entire pool of alleles. Since we know that 30% of the population's alleles are for blue hair, this means that out of a large population of Moms, on average 30% will give their kids a blue allele. So will 30% of Dads. And so on.

This would NOT work if the gene was sex-linked, or if reproducers sought out mates that were similar to themselves (or different from themselves, for that matter). The ONLY reason we can continue with the calculations below is because we're assuming that the alleles an offspring inherit are in fact random and therefore represent the allele pool. So, without further ado, back to our regularly scheduled program...

What is the probability that an offspring gets 2 blue alleles? (mouse over these images for the answers!)

Or both brown, that should be easy...

As for the silent carrier, what happens if one parent donates a blue allele and one donates a brown allele...

DESC

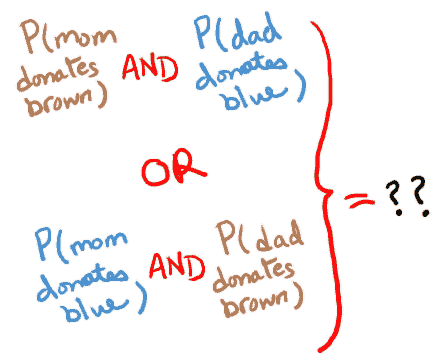
The Assistant returned triumphantly, "Exactly (on average) 49% should be unaffected, 42% carriers, and 9% blue."

The ME gave a nasty smirk and held up an official looking report. "Oh, but according to the latest-latest research, only 22% of the allele pool actually codes for the blue-hair trait. How does that change your predictions?"

harvey wallbanger with orange slice"OK, give me a minute to write some probability equations. Can I use that for scrap paper? " muttered the Assistant.

The ME tossed over the report. "You might want to look up the Hardy Weinberg Equilibrium."

"Harvey Wallbanger?" asked the Assistant.

"No, that's a drink which makes it harder to keep your equilibrium..."