>Episode 2: Hardy and Weinberg to the rescue
Finding q
|
After escaping the OA by saying he had work to do, the Assistant slipped into his office. He had just started to play a game of hangman when the phone rang. "Get down to the Swedish Hospital and Hair Academy ," roared the ME. "It seems that blue-hair syndrome has appeared there as well. A full 40% of the patient population has blue hair. The Academy would like to determine what the actual prevalence of the gene is, and how common carriers are." "I'm on it like a blue light special," promised the Assistant. |
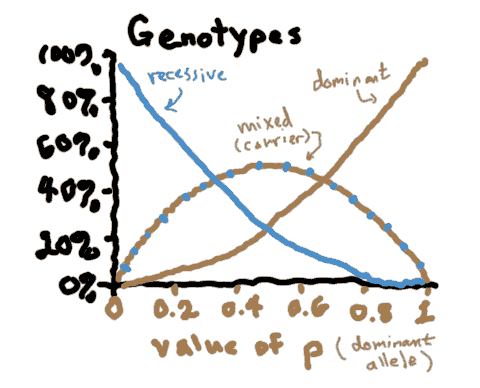
Just by observing a population, you can't tell how many carriers there are, but you can tell how common the homozygous recessives are (in this case, blue-haired people).
So, is it possible to determine the actual prevalence of an allele (i.e., the value of p) if you only know the how many recessive phenotypes are out there? (This being a math module, obviously the answer is yes...)
| One way to do this would be to look at the graph we made before. If 40% of the population has blue hair, then approximately what is q? | 
|
(Roll your mouse over the graph to see this.) So the answer looks like p = about 0.35, and q = about 0.65. But its pretty hard to be exact. So, as the Assistant would say, let's try some algebra. |
What is q, assuming that 40% of the population shows the recessive trait?
(To make this problem interactive, turn on javascript!)
- I need a hint ... : What proportion of the population exhibits the recessive trait, in terms of p and q?
- ...another hint ... : Since q2 is the proportion of the population exhibits the recessive trait, and q2 = 40%, what mathematical operation would allow you to find q?
- ...If you get a number that's much too small... : You need to express 40% as a number between 0 and 1 (a proportion).
The problem is that percentages are really fractions, so taking a square root is not simple -- you can tell that the answer is wrong if q is way too low, like 6%.
I think I have the answer: Square root(.40) = 0.63
How common are carriers, assuming that 40% of the population shows the recessive trait?
(To make this problem interactive, turn on javascript!)
- I need a hint ... : You already found q in the last problem (0.63).
- ...another hint ... : If you know q, you can also find p...
I think I have the answer: 2*0.37*0.63 = 0.47, or 47%
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: admin@mathbench.umd.edu