Table of Contents

• Section 1. How the meningitis population grows
• 1: How many meningococci can kill you?
• 2: Build the basic growth equation
• 3: Draw exponential growth
• Section 2. So why isn't Frank dead already?
• 4: How long has poor Frank got?
• 5: All we need now is data
• 6: Looking at data
• 7: Log transform straightens out exponential growth
• 8: Do ALL curves get "straightened" by taking the log?
• 9: Phases of bacterial growth
• Section 3. How can we tell when the population is growing exponentially?
• 10: A test for exponential growth
• 11: And the answer is...
• 12: No way its growing that fast!
• 13: Some more practice
• 14: Extended problem: Exponential growth ends
• 15: Review

Review

The dose of a drug or contaminant that is likely to kill you is called the LD50 (lethal dose for 50% of the population). The LD50 for meningitis is about 500 cells/mL blood, and we canscale up from there to determine that about 2.5 million cells are needed in the entire body. It would take about 20 to 21 generations of doubling for a population starting from a single meningococcal cell to reach 2.5 million cells.

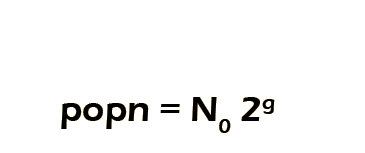Exponential growth follows the pattern

• # in gen₀ --> 1
• # in gen₁ --> 1*2
• # in gen₂ --> 1*2*2
• # in gen₃ --> 1*2*2*2

The (untransformed) graph is a line curved up. When the graph is log-transformed, it becomes a straight line (pointing up, assuming the population is growing). This happens because during exponential growth, the population always grows by the same factor (multiplier).

Using knowledge about how the log-transformed graph appears, we can determine whether a bacterial population is in a lag, log, stability, or death phase.

We can determine doubling time roughly by reading it off a graph. To do this, pick a starting population (on the y axis) which falls within the exponential growth window. Find the doubled population and check that it also falls within the exponential growth window. Find the amount of time elapsed (on the x axis) between the two population readings. This is the approximate doubling time.

Another way to estimate doubling time would be to calculate it based on data about how long it takes to get to LD50, and how many generations that represents.

The original doubling time we calculated, based on lab data from growing meningococci in an ideal media, was too fast. Other factors are at work here. Luckily for Frank...