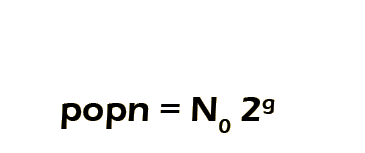MathBench > Microbiology

Frank's Football Fiasco

Build the basic growth equation

As you know, bacteria multiply by dividing, so to speak. A single bacterium grows and then divides into 2. Those two "daughter" cells eventually divide in 2. And so on.

cells divideThe equation for exponential growth should be familiar to you. Starting with one cell dividing in half, the resulting numbers would look like this:

# in gen0 --> 1

# in gen1 --> 1*2

# in gen2 --> 1*2*2

# in gen3 --> 1*2*2*2

# in gen4 --> 1*2*2*2*2

Instead of writing "# in gen 4", it is more usual to write N(4). Likewise, for the general equation we write N(t). So, given the formulas above, which of the following is the correct equation for exponential growth starting from a single cell and continuing for g generations?

N(g) = g * 2g N(g) = 1 * 2g N(g) = 1 * 2g N(t) = 1 * g2

With a few more changes, we can make this look more official.

  1. Most importantly, Frank may not have been so lucky as to start with one single, solitary invading meningococcus. Maybe, despite his killer immune system, he had 2, or even 3. So, instead of the initial population being 1, let's call it N0, pronounced "n sub zero", meaning "the number of cells in generation 0". (This is also really important when we're talking about lab populations that may have started with much larger numbers).

  2. Less importantly, I removed the multiplication sign - it's still there, just invisible.

Our final equation looks like this: (mouse over for more info!)