Extended problem:
Exponential growth ends (with a whimper)
Here's a second set of data on meningococcal growth rates. Your instructions are
1) to determine the exponential growth rate of the bacteria, and
2) to determine when growth stops being exponential.
| time | popn |
|---|---|
| 0 min | 4.3 * 106 |
| 20 min | 9.7 * 106 |
| 40 min | 22 * 106 |
| 60 min | 48 * 106 |
| 80 min | 97 * 106 |
| 100 min | 116 * 106 |
| 120 min | 118 * 106 |
| 140 min | 67 * 106 |
Just look at the data first... what can you see with your bare eyes, so to speak?
About doubling time:
About the general shape of the population trajectory:
About when growth begins to slow down:
Now try plotting the data.
Which time period showed exponential growth:
Let's look at an untransformed graph to figure out the doubling time. We could do this on the log-transformed graph above, but its difficult because the y-axis is on a log scale.
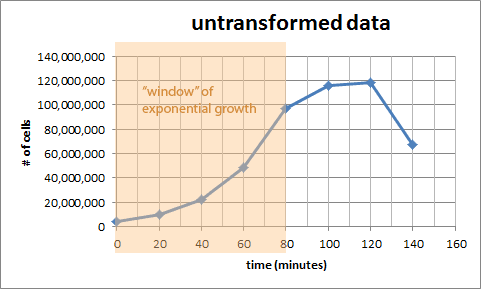
Where should we start, and what is the growth rate?
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu