MathBench > Cellular Processes

Diffusion through a Membrane

Equation deja vu

Remember back in the diffusion module, we used an equation to relate the rate of diffusion to the steepness of the concentration gradient? Well, in case you've forgotten, that equation was:

Continuous form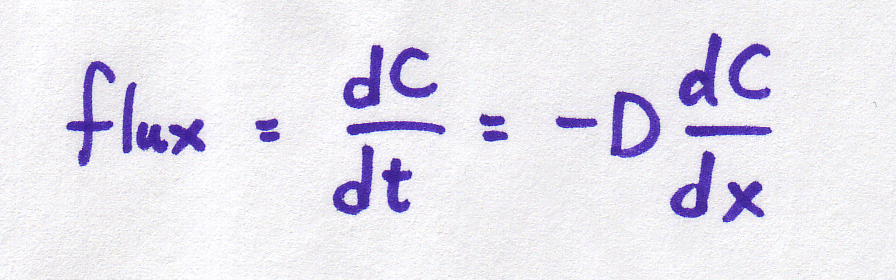

and we also discussed how this "continuous" equation can be made into a "discrete" equation:

Discrete form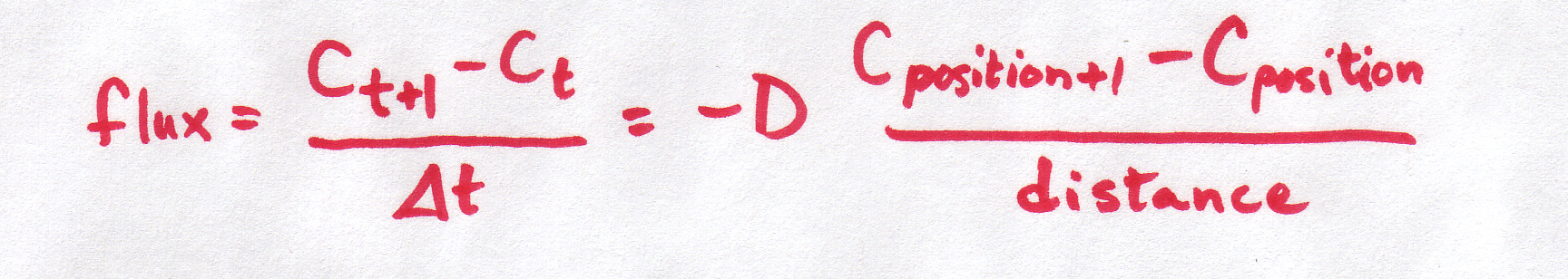

It is important to understand that BOTH of these equations refer to the same basic phenomenon -- particles moving at random, with the net result that particles move from areas of high concentration to areas of low concentration. And BOTH of these equations describe what's happening in the same way -- the concentration gradient is defined by the difference in concentrations per distance between them.


So why are we using two different equations for the same thing??? Sometimes, a discrete equation is an "easier" version of a continuous equation, and sometimes it's the other way around, the continuous is an "easier" version of the discrete. In this case, the discrete is easier, but the continuous is more realistic. The discrete is an approximation or simplification of reality. The discrete equation tells us a lot about the process without needing to get involved in the truly messy kind of math required to work with the continuous version (which require partial differential equations -- look them up if you want to know more!).

In this module, we'll learn something about osmosis, potential differences, and pressure gradients, but we'll also talk a lot about discrete vs. continuous equations, and algebra vs. calculus.

Clipart for this module thanks to Arthur's Clipart, FreeImages.co.uk, Clipart Heaven