Extended problem #2: Exponential growth ends (with a whimper)
Enough with the cute little stories. The last few pages are all biology, all the time. I put some of the basic exponential growth information in the box to the right, and the rest is for you to figure out.
Helpful Info on
Exponential Growth:
Nt = N0 * 2g
Nt = N0 * e(mt)
m = ln(2)/doubling time
As you know, bacterial cultures go through several growth phases. In the beginning, when resources are extremely plentiful, bacteria grow exponentially, but growth slows as the environment gets more crowded and resources are harder to find. Eventually as resources get used up, the population levels out and then declines. So, your job is to figure out when the exponential part of growth is over.
You have been given a mystery bacteria and growth medium by your instructor. Your instructions are 1) to determine the exponential growth rate of this bacteria, and 2) to determine how long the medium continues to support exponential growth. Specifically, you will know when the bacteria are no longer growing exponentially because their population size is less than 90% of what would be predicted by exponential growth.
Here is the data from your growth experiment:
| time | popn |
|---|---|
| 0 min | 4.3 * 106 |
| 20 min | 9.7 * 106 |
| 40 min | 22 * 106 |
| 60 min | 48 * 106 |
| 80 min | 97 * 106 |
| 100 min | 116 * 106 |
| 120 min | 118 * 106 |
| 140 min | 67 * 106 |
Just look at the data first... what can you see with your bare eyes, so to speak?
About doubling time:
About the general shape of the population trajectory:
About when growth begins to slow down:
What is the growth rate? (this is a simplified way to calculate the growth rate -- you can also review page 9 for how to calculate doubling rate, and use that to get the growth rate)
(To make this problem interactive, turn on javascript!)
- I need a hint: Use the first 2 timesteps
- ... another hint ... : In the equation Nt = N0 * emt, you know everything but "m" (the growth rate), so plug it all in.
- ... another hint ... : Remember, logs are a biologist's best friend (a.k.a. when you have trouble with exponents, try logs)
- ... still more ... : try using ln on both sides (to get rid of the e) and then solving for m
- ... last chance ... : ln(Nt / N0) = mt
I think I have the answer: ln(9.7/4.3) / 20= 0.041 per min
What should the population be at the third time measured?
(To make this problem interactive, turn on javascript!)
- I need a hint: Its hard to use doubling time, but easy to use the growth rate "m"
- ... another hint ... : Which equation will give you the predicted population size at time ...
- ... last chance ... : plug all the known values into Nt = N0 * emt
I think I have the answer: 4.3 * 106 * e0.041*40 = 2.22 * 107
When did exponential growth stop?
(To make this problem interactive, turn on javascript!)
- time = 40 min ?: No...we just calculated a predicted population of 22.2 million, which is very close to one in the table.
- time = 60 min ?: No... the predicted population at time = 60min is 50.3 million, again quite close to 48 million.
- time = ... 80 min ?: maybe... The predicted population at time = 80min is 114 million, whereas the actual population was 97 million
- find the %: 97 million / 114 million = 0.85 = 85%
- ...last chance...: The population only grew to 85% of its expected size -- below our 90% cutoff for exponential growth.
I think I have the answer: time = 80 min
Judging exponential growth...
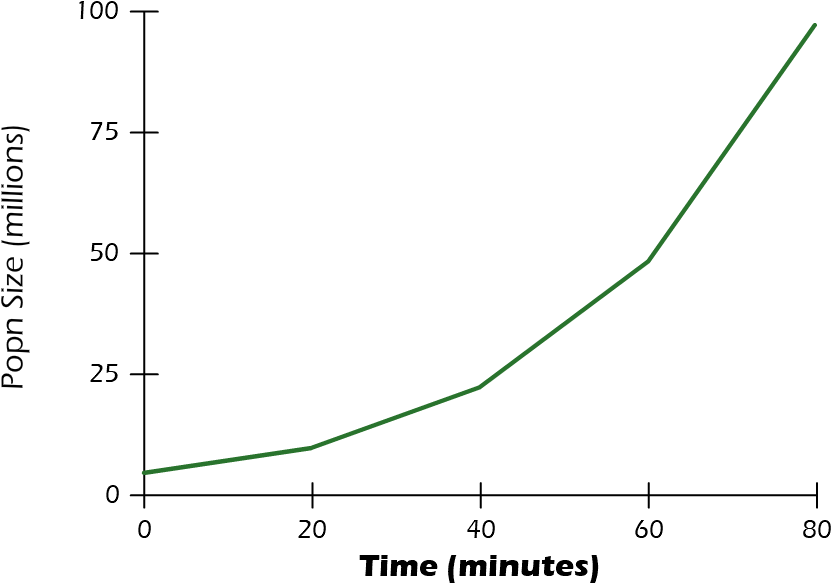
If you just look at the first part of the actual population data over time, it is hard to tell whether or not it is exponential. In this early growth stage, the graph appears to increase like an exponential graph.
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu