Simpson’s Dominance Index
You might have noticed that when the community was dominated by just 2 species, the Simpsons-Dominance Index is just about one-half. Let's see if that's a coincidence:
| Species percents | Adding the squares... | Simpson's Dominance |
|---|---|---|
| 50%, 49%, 1% | .25 + .24 + .0001 | .4901 |
| 50%, 48%, 1%, 1% | .25 + .23 + .0001 + .0001 | .4802 |
| 50%, 47%, 1%, 1%, 1% | .25 + .22 + .0001 + .0001 + .0001 | .4703 |
So as we add each additional (but barely present) species, Simpson's Dominance declines a little -- but not much. It's still pretty close to 1/2.
Now let's try it with a 3-species community.
| Species percents | Adding the squares... | Simpson's Dominance |
|---|---|---|
| 33%, 33%, 33%, 1% | .109 + .109 + 1.09 + .0001 | |
| 33%, 33%, 32%, 1%, 1% | .109 + .109 + 1.02 + .0001 + .0001 | |
| 33%, 33%, 31%, 1%, 1%, 1% | .109 + .109 + 0.96 + .0001 + .0001 + .0001 |
Same deal -- Simpson's Dominance is about 1/3 in a community dominated by 3 species -- but it declines a little for each new species added.
So unlike richness or %dominance, Simpson's Dominance is a very flexible measurement that takes the entire community into account.
Let's try just one more:
 What is the Simpson’s Dominance Index for a stream if 55% of what you find is blackfly larvae, and there are 9 other species that each are found 5% of the time?
What is the Simpson’s Dominance Index for a stream if 55% of what you find is blackfly larvae, and there are 9 other species that each are found 5% of the time?
(To make this problem interactive, turn on javascript!)
- I need a hint ... : .552 + .052 + .052 + .052 + .052 + .052 + .052 + .052 + .052 + .052=
- ...another hint ... : 0.3025 + 9* 0.0025
I think I have the answer: 0.325
So the Simpson's Dominance Index is telling you that this community (dominated by blackflies, but containing even amounts of 9 other species), is similar to a community with 3 dominant species and not much else. Does this prove anything? Not really -- just because the math works out does not mean that nature has to operate that way. However, it does raise some interesting (and testable) questions about how multi-species communities function.
Note: Usually Simpson's Diversity Index is reported, instead of Simpson's Dominance Index. Once you have Simpson's Dominance Index, all you need to do is subtract it from 1. With Simpson's Diversity, as the community gets more even and diverse, the score goes up. So, up is good.
Here is the Scary-looking Official Equation for Simpson's Diversity Index: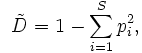
Reading this equation from right to left, you need to
- square each percentage
- add up all the squares
- subtract from one
Although Simpson's Diversity is more common in the literature, we will use Simpson's Dominance in this module because it's a little simpler.
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu