MathBench > Cellular Processes

Diffusion

Why do rhinos have lungs and amoebas don't?


This sounds like a question for kindergarten "Why don't amoebas have lungs? - Because they're too small!" But let's think about it a little more. What is the function of a lung? Bringing oxygen into the body and expelling carbon dioxide. When I contract my diaphragm, my lungs expand and air (with oxygen) gets sucked in. When I relax my diaphragm, the lungs contract and air gets pushed out.

 

Another way to say this is that gases move into and out of lungs through bulk flow (the details are different for other animals, who may have lungs, gills, spiracles, whatever). Do amoebas need to exchange gases? Of course, they respire just like the rest of us. So why don't amoebas require advection to exchange gases?

OK, you've probably figured out the answer, having just read an entire module on diffusion. Amoebas are small, oxygen and carbon dioxide are small molecules, and we’ve said that diffusion works well for small molecules over short distances.

How small and how short? Recall that T = x2 / 2D

A humongous amoeba might be measure as much as 0.02 cm in diameter. That means from the outside to the center of the cell is at most 0.01 cm.

And here are some representative values of D:

Molecule and Medium

D (cm2/sec)

Oxygen in air

1.0 x 10-1

Oxygen in water

1.8 x 10-5

Protein in water

1.0 x 10-6

Phospholipid in water

1.0 x 10-8

We'll use 10-5 as the diffusion coefficient for calculations in this section.

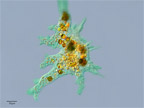amoebaHow long (at most) should it take oxygen to diffuse throughout the amoeba?

(To make this problem interactive, turn on javascript!... may not work in Internet Explorer )

I think I have the answer: T = X 2 / 2D =
(0.01cm)2 / (2*10-5cm2/sec ) =
5 sec