And SMALL numbers?
Consider an E. coli ... measuring 0.000002 m. It would be easy to say log(0.000001) = −6 ... but
E. coli are bigger than that. Not big enough to get to a log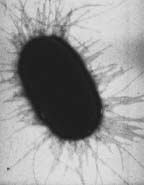 
scale number of −5, but
about a tenth of the way between − 6 and − 5. If you imagine a number line, you'll see that:
a tenth of the way between −6 and −5 = −5.9
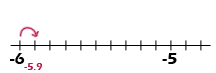
If we do some "exaggerating", we might guess −5.8 or even less. In fact,
log(0.000002) = −5.7 (E. coli)
Likewise, red blood cells have a diameter of 0.000007 m, so they are also between minus 6 and minus 5 on a log scale:
log(0.000007) = −5.2 (red blood cell)
You can tell that E. coli are smaller than red blood cells, because −5.7 is smaller than −5.2.
Now that we know that normal red blood cells are approximately −5.2 on a log scale, we can also guess that a blood cell that is a −4 is going to be very problematic for the poor creature whose capillaries get exploded by it. And a red blood cell that's a −6 will be too tiny to do any good.
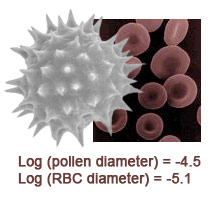
A red blood cell diameter is −5.2 on the log scale, while a typical pollen grain is a −4.5. Which is smaller?
(To make this problem interactive, turn on javascript!)
- I need a hint ... : The more negative the log, the smaller the measurement.
- ...another hint ... : The log of red blood cell diameter is more negative
than the log of pollen grain diameter, so it must be smaller.
I think I have the answer: The red blood cell is smaller.
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu