Table of Contents

• Prequiz...
• Everything you always wanted to know about logs (but were too bored to ask)
• 1: When size matters
• 2: There must be a better way!
• 3: Special numbers
• 4: The log is the power!
• 5: What about messy numbers?
• 6: And SMALL messy numbers?
• 7: Your turn with messy numbers
• 8: Antilogs
• So what are they good for?
• 9: Measuring earthquakes
• 10: Measuring acidity
• 11: Differences in acidity
• Review
• 12: Summary

The log is the power!

In the last few screens, we saw that finding a log (at least for easy, powers-of-ten numbers) can be done by counting the zeros. "Counting the zeros" is the same as saying "what power would I need to raise 10 to in order to get this measurement?" That's important, but hard to remember. A shorter version is ... "the log is the power".

 

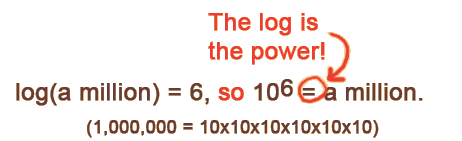Likewise, if your chances of winning the lottery are 1-in-a-million ( = 0.000001), we could say that

 

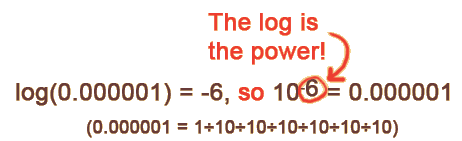Keep in mind that "the log is the power" as you look at the formal mathematical definition of logarithm to the base 10 (log10):

If x= 10^y then y = log x

The log₁₀ of a number is the power to which 10 must be raised to give that number.

For example 100 = 10 × 10 = 10², and 2 = log(100).

 

 

You can use the applet below to practice finding the log of easy (non-messy) numbers. Keep at it until it becomes very easy!