MathBench > Cellular Processes

Osmosis

What else can the equations tell us?

Continuous form
Discrete form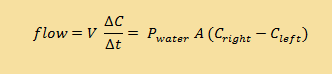


Here are a few last questions on interpreting the equations:

What will the rate of water flow be if permeability is zero?

(To make this problem interactive, turn on javascript!)

I think I have the answer: No matter how high the difference in osmolarity, no osmosis will occur if the permeability is 0. For example, osmosis will not work through a brick wall


When will the rate of water flow be the highest?

(To make this problem interactive, turn on javascript!)

I think I have the answer: Assuming that area (A) is constant, you need the permeability (P) to be as high as possible. You also need the difference in osmolarity (C right - C left) to be as high as possible -- for example, one side pure water with OsM=0, and the other side with as high osmolarity as possible.


What happens if the osmolarity of the two solutions is the same (if they are iso-osmotic)?

(To make this problem interactive, turn on javascript!)

I think I have the answer: If the two sides have the same concentrations, then
then (C right- C left) = 0, and NO net osmosis will take place, no matter how large or leaky your membrane is.

None of these were really rocket science. The point is that the equation for rate of water flow is simply a formalisation of what our intuition tells us should happen. The equation puts intuition into mathematical language!