Interpreting the chi-square test
So, once you know the degrees of freedom (or df), you can use a chi square table like the one on the right to show you the chi-square-crit corresponding to a p-value of 0.05. That's the whole detour summed up in one sentence. Whew. For the workweek test, with 1 df , the chi-square-crit is 3.84, whereas his chi-square-calc was 0.167. What does critical value mean?
|
 |
Basically, if the chi-square you calculated was bigger than the critical value in the table, then the data did not fit the model, which means you have to reject the null hypothesis. 
On the other hand, if the chi-square you calculated was smaller than the critical value, then the data did fit the model, you fail to reject the null hypothesis, and go out and party.*
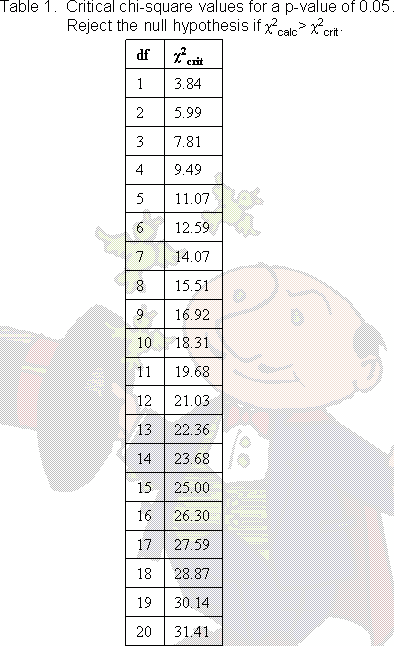Why do you think the chi-square-crit increases as the degrees of freedom increases?
(To make this problem interactive, turn on javascript!)
- I need a hint ... : If you have, say, 15 degrees of freedom,
how many rows are in your table?
- ...another hint ... : For every row in the table you need to calculate another deviation.
I think I have the answer: With a lot of degrees of freedom,
you have a lot of rows in your table. Therefore you're adding
more numbers together to get your final chi-square.
So it makes sense that the critical value also increases.
Fine print: some chi-square lookup tables have many columns, one for each p-value you might be interested in. In that case, you first need to find the 0.05 p-value (or any other p-value you're asked for), then the df, then the chi-square-crit.
Even finer print: or, you may be asked to find the p-value corresponding to the chi-square-calc. In that case you have to find the right df first, then find the two chi-square-crits that your chi-square-calc falls between, then note the p-value.
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu