Extended problem #1: E. coli ate my lab report
You and your TAs both get lectured about keeping your samples uncontaminated. Why? Is it because you are likely to grow E. coli so monstruous that they threaten to devour your lab bench and escape to nearby spinach fields? Actually, believe it or not, that's not the real problem.
The real problem is much more mundane. You've heard the expression "finding a needle in a haystack?" Well, the E. coli that you might contaminate your petri dish with are the proverbial haystack.
Let's say you are trying to culture a bacterium that doubles every 2 hours. But unwittingly, you have introduced a tiny amount of E. coli into your culture. Just 1%. How much difference could it make???!
To make things easy, assume that E. coli doubles every 20 minutes. How do matters stand when you come back 8 hours later?
What's your needle-to-haystack ratio?
(To make this problem interactive, turn on javascript!)
- The needle: start with 99 target bacteria and double every 2 hours -- how many do you end up with?
- The haystack : Start with 1 E coli and double evey 20 minutes -- how many do you end up with?
- The ratio : Now take the ratio...
I think I have the answer: 17 million / 1600 =
approx 1 in 10,000
Wow. (Insert stronger language here). Good luck finding that needle.
Here's the same problem with a twist -- messy numbers! We'll go back to making yogurt. Recall that a typical yogurt culture has a doubling time of about 55 minutes.
Sadly, the spinach in your quiche lorraine yogurt was contaminated at 0.1% with a virulent strain of E. coli, doubling every 23 minutes. After 24 hours of incubation, what do you find?
(To make this problem interactive, turn on javascript!)
- Simplify those messy numbers: by finding the growth rates per minute.
- Find the initial conditions: 1 out of 1000 was E. coli, so that means 999 were yogurt culture.
- The needle : Now grow your yogurt for 24*60 minutes.
- The haystack : And the E coli...
- The ratio: 7*1018 / 8 * 1010 = approx 108
I think I have the answer: about 100 million to 1 E coli
Here is an applet that demonstrates the same thing. See if you can figure out when would be the best time to check on the yogurt...
Contamination
Your yogurt culture has a doubling time of 55 minutes and a starting population 1000 times larger than E. coli.
Yogurt: N(t) = 999 * e0.01t
E. coli: N(t) = 1 * e0.03t
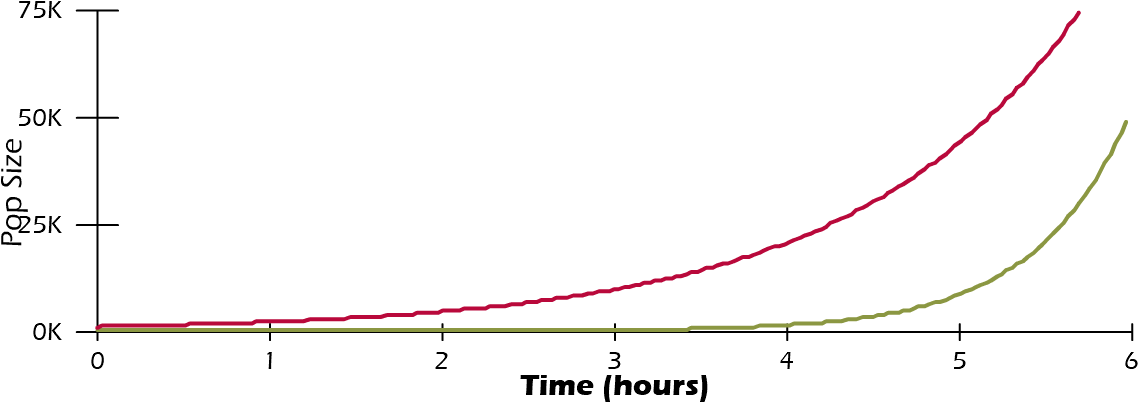
How long will it take E. coli (green for spinach, get it?) to reach 10% of the total culture?
Prediction: hours
Check your estimate by selecting the Check button.
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu