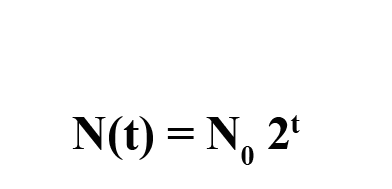MathBench > Population Dynamics

Bacterial Growth:
The E. coli ate my homework

Building the basic growth equation

As you know, bacteria multiply by dividing, so to speak. A single bacterium grows and lengthens, and then divides into 2. Those two "daughter" cells eventually divide in 2. And so on.

The equation for exponential growth should be familiar to you. Starting with one cell dividing in half, the resulting numbers would look like this:

# in gen0 --> 1

# in gen1 --> 1*2

# in gen2 --> 1*2*2

# in gen3 --> 1*2*2*2

# in gen4 --> 1*2*2*2*2

Instead of writing "# in gen 4", it is more usual to write N(4). Likewise, for the general equation we write N(t). So, given the formulas above, which of the following is the correct equation for exponential growth starting from a single cell?

N(t) = t * 2t N(t) = 1 * 2t N(t) = 1 * 2t N(t) = 1 * t2

With a few more changes, we can make this look more official.

  1. Most importantly, we may not be so lucky as to start with one single, solitary cell. The culture could start with 2, or 7, or 10,000. Instead of the initial population being 1, let's call it N0, pronounced "n sub zero", meaning "the number of cells in generation 0".

  2. Less importantly, I removed the multiplication sign - it's still there, just invisible.

Our final equation looks like this: (mouse over for the definitions of these variables!)