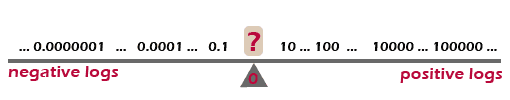Table of Contents

• Prequiz...
• Everything you always wanted to know about logs (but were too bored to ask)
• 1: When size matters
• 2: There must be a better way!
• 3: Special cases
• 4: The log is the power!
• 5: What about messy numbers?
• 6: And SMALL messy numbers?
• 7: Your turn with messy numbers
• 8: Antilogs
• So what are they good for?
• 9: Measuring acidity
• 10: Measuring the power of an earthquake
• 11: pH again
• Review
• 12: Important Things to Remember about Logs

There must be a better way!

Indeed there must. Scientists often use an alternative numbering system called a "log" scale. When you put a number on a log scale, you are basically saying "how many zero's are in that number?"

log size 5 needed -- to hold 5 zeros. Log(100,000) = 5

log size 9 needed -- to hold 9 zeros. Log(1,000,000,000) = 9

 

So, for 1 followed by a bunch of zeros, the log just tells you how many zeros there are. As a further example, a "google" is 1 followed by 100 zeros. Therefore, log(google) = 100! (That would be a pretty big log).

Now let's get a little more general. After all, not all numbers end in a bunch of zeros. Although number like 10,000 "takes up space" before the decimal point, a number like 0.00001 "takes up space" AFTER the decimal point. In a sense, that's space taken up in the "opposite" direction. We show that by making the log negative rather than positive. So,

	= 4 (count the zeros after the first digit)
	= -4 (count the decimal point and the zeros after it, but stop when you get to a non-zero digit)

 

So big numbers produce positive logs and small numbers produce negative logs. There must also be a log that is exactly 0, right? So what is the balancing point between big and small numbers? Mouse over the image below to see if you are correct:

 

SOME FINE PRINT THAT YOU STILL SHOULDN'T SKIP: This module talks about log base 10 -- there are other bases, notably log base 2 used in computers, and the natural log, used in any science that deals with growth or decay. However, log base 10 is a common base and arguably the easiest to understand. When using your calculator, you may have keys labeled "LOG" (for log base-10) and "LN" (for natural log). You want to use the log key, not the LN key. When in doubt, check that log(10) = 1. END OF FINE PRINT

How about an example already?

The stars in our galaxy: a hundred billion is a 1 with 11 zeros after it, so the log scale version of this number is simply 11.

log(100,000,000,000) = 11

 

Your chances of winning the lottery: let's say it's one-in-a-million. Expressed as a decimal, that is 0.000001. So, count the decimal place and the zeros AFTER it, and stop when you get to the non-zero digit:

log(0.000001) = -6